Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(2,\\ a,PT\Leftrightarrow\sqrt{\left(5x-1\right)^2}=\sqrt{4\left(x+1\right)^2}\\ \Leftrightarrow\left|5x-1\right|=2\left|x+1\right|\\ \Leftrightarrow\left[{}\begin{matrix}5x-1=2\left(x+1\right)\\1-5x=2\left(x+1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=3\\7x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{7}\end{matrix}\right.\)
\(b,ĐK:x^2-3\ge0\\ PT\Leftrightarrow\sqrt{x^2-3}=x-1\\ \Leftrightarrow x^2-3=x^2-2x+1\\ \Leftrightarrow2x=4\Leftrightarrow x=2\left(tm\right)\\ c,ĐK:x\le\dfrac{7}{2}\\ PT\Leftrightarrow7-2x=x^2+7\\ \Leftrightarrow x^2+2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\\ d,ĐK:x\ge3\\ PT\Leftrightarrow3\sqrt{x-3}+\dfrac{1}{2}\cdot2\sqrt{x-3}-9\cdot\dfrac{1}{3}\sqrt{x-3}=2\\ \Leftrightarrow\sqrt{x-3}=2\\ \Leftrightarrow x-3=4\Leftrightarrow x=7\left(tm\right)\)

bạn nên tự nghiên cứu rồi giải đi chứ bạn đưa 1 loạt thế thì ai rảnh mà giải, với lại cứ bài gì không biết chưa chịu suy nghĩ đã hỏi rồi thì tiến bộ sao được, đúng không

a) Ta có: \(A=3\sqrt{20}-\sqrt{45}+2\sqrt{18}+\sqrt{72}\)
\(=6\sqrt{5}-3\sqrt{5}+6\sqrt{2}+6\sqrt{2}\)
\(=3\sqrt{5}+12\sqrt{2}\)
b) Ta có: \(B=\dfrac{12}{3-\sqrt{5}}-\dfrac{16}{\sqrt{5}+1}\)
\(=\dfrac{12\left(3+\sqrt{5}\right)}{4}-\dfrac{16\left(\sqrt{5}-1\right)}{4}\)
\(=3\left(3+\sqrt{5}\right)-4\left(\sqrt{5}-1\right)\)
\(=9+3\sqrt{5}-4\sqrt{5}+4\)
\(=13-\sqrt{5}\)
c) Ta có: \(C=10\sqrt{\dfrac{1}{5}}+\dfrac{1}{5}\sqrt{125}-2\sqrt{20}\)
\(=\dfrac{10}{\sqrt{5}}+\dfrac{1}{5}\cdot5\sqrt{5}-2\cdot2\sqrt{5}\)
\(=2\sqrt{5}+\sqrt{5}-4\sqrt{5}\)
\(=-\sqrt{5}\)
e) Ta có: \(E=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\sqrt{3}+1-2+\sqrt{3}\)
\(=2\sqrt{3}-1\)
f) Ta có: \(F=\sqrt{6+2\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{5}+1-\sqrt{5}+2\)
=3

e) Ta có: \(E=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\sqrt{3}+1-2+\sqrt{3}\)
\(=2\sqrt{3}-1\)
f) Ta có: \(F=\sqrt{6+2\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{5}+1-\sqrt{5}+2\)
=3
a) Ta có: \(A=3\sqrt{20}-\sqrt{45}+2\sqrt{18}+\sqrt{72}\)
\(=6\sqrt{5}-3\sqrt{5}+6\sqrt{2}+6\sqrt{2}\)
\(=3\sqrt{5}+12\sqrt{2}\)
b) Ta có: \(B=\dfrac{12}{3-\sqrt{5}}-\dfrac{16}{\sqrt{5}+1}\)
\(=\dfrac{12\left(3+\sqrt{5}\right)}{4}-\dfrac{16\left(\sqrt{5}-1\right)}{4}\)
\(=3\left(3+\sqrt{5}\right)-4\left(\sqrt{5}-1\right)\)
\(=9+3\sqrt{5}-4\sqrt{5}+4\)
\(=13-\sqrt{5}\)

1: \(=\sqrt{5}-\dfrac{\sqrt{5}}{2}=\dfrac{\sqrt{5}}{2}\)
2: \(=\dfrac{4+2\sqrt{3}+4-2\sqrt{3}}{2}=\dfrac{8}{2}=4\)
4: \(=\dfrac{-3+5\sqrt{3}}{11}+\dfrac{3+5\sqrt{3}}{11}=\dfrac{10\sqrt{3}}{11}\)

\(1,=2\sqrt{3}-3\sqrt{3}+4\sqrt{3}=3\sqrt{3}\\ 2,=\left(2\sqrt{6}+2\sqrt{5}-4\sqrt{5}\right):5=\dfrac{2\sqrt{6}}{5}-\dfrac{2\sqrt{5}}{5}\\ 3,=6\sqrt{3}-\dfrac{4\sqrt{3}}{3}-4\sqrt{3}-\dfrac{5\sqrt{3}}{3}=2\sqrt{3}-\dfrac{9\sqrt{3}}{3}=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\\ 4,Sửa:\dfrac{1}{\sqrt{5}-\sqrt{3}}-\dfrac{1}{\sqrt{5}+\sqrt{3}}\\ =\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{5}+\sqrt{3}}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\)
1) \(=2\sqrt{3}-3\sqrt{3}+4\sqrt{3}=3\sqrt{3}\)
2) \(=\left(2\sqrt{6}+2\sqrt{5}-4\sqrt{5}\right)=\dfrac{2\sqrt{6}}{5}+\dfrac{2\sqrt{5}}{5}-\dfrac{4\sqrt{5}}{5}\)
3) \(=6\sqrt{3}-\dfrac{4\sqrt{3}}{3}-4\sqrt{3}-\dfrac{5\sqrt{3}}{3}=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\)
4) \(=\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{5}+\sqrt{3}}{5-3}=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\)

1) \(A=2\sqrt{5}-6\sqrt{2}+3\sqrt{5}=5\sqrt{5}-6\sqrt{2}\)
2) \(B=\dfrac{30\left(\sqrt{7}+1\right)}{7-1}+\dfrac{15\left(\sqrt{7}-2\right)}{7-4}=5\sqrt{7}+5+5\sqrt{7}-10=-5+10\sqrt{7}\)
3) \(C=\left(3-\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\right)\left(3+\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\right)=\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)=9-5=4\)
4) \(D=3-\sqrt{2}+1-\sqrt{2}=4-2\sqrt{2}\)
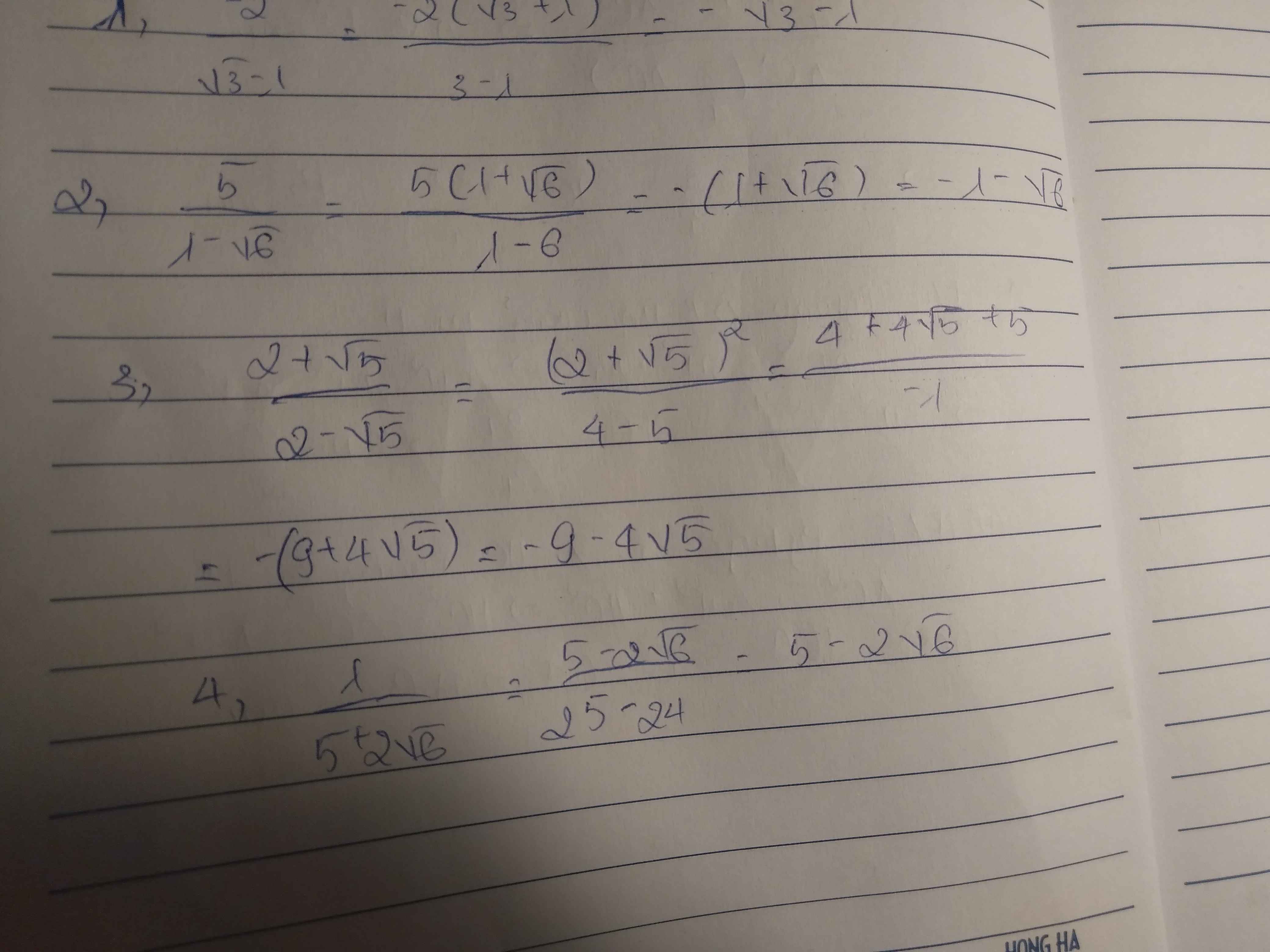
a) \(\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}=\sqrt{2}+1-\left(\sqrt{2}-1\right)=2\)
b) \(\dfrac{1}{\sqrt{3}-1}-\dfrac{1}{\sqrt{3}+1}=\dfrac{\sqrt{3}+1-\left(\sqrt{3}-1\right)}{3-1}=1\)
c) \(2\sqrt{5}-3\sqrt{45}+\sqrt{500}=2\sqrt{5}-9\sqrt{5}+10\sqrt{5}=3\sqrt{5}\)
d) \(\dfrac{1}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}=\dfrac{1}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{4}\right)}{\sqrt{5}-2}=\dfrac{1}{\sqrt{3}+\sqrt{2}}-\sqrt{3}=\dfrac{1-\sqrt{3}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}=\dfrac{1-3-\sqrt{6}}{\sqrt{3}+\sqrt{2}}=\dfrac{-2-\sqrt{6}}{\sqrt{3}+\sqrt{2}}=\dfrac{-\sqrt{2}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}=-\sqrt{2}\)
e) \(\dfrac{1}{2+\sqrt{3}}-\dfrac{1}{2-\sqrt{3}}+5\sqrt{3}=\dfrac{2-\sqrt{3}-\left(2+\sqrt{3}\right)}{4-3}+5\sqrt{3}=-2\sqrt{3}+5\sqrt{3}=3\sqrt{3}\)
f) \(\sqrt{3}-\sqrt{4+2\sqrt{3}}=\sqrt{3}-\left(\sqrt{3}+1\right)=-1\)
g) \(\dfrac{5-\sqrt{5}}{\sqrt{5}-1}-\dfrac{4}{\sqrt{5}+1}=\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}-\dfrac{4}{\sqrt{5}+1}=\sqrt{5}-\dfrac{4}{\sqrt{5}+1}=\dfrac{5+\sqrt{5}-4}{\sqrt{5}+1}=1\)
h)\(\sqrt{37-20\sqrt{3}+\sqrt{37+20\sqrt{3}}}=\sqrt{37-20\sqrt{3}+\left(5+2\sqrt{3}\right)}=\sqrt{42-18\sqrt{3}}=\sqrt{\left(3\sqrt{3}+3\right)^2+6}\)