Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)

Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)

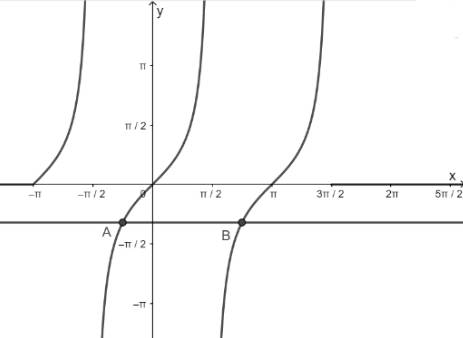
a) Hàm số y = tanx nhận giá trị bằng – 1
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = tanx và y = - 1
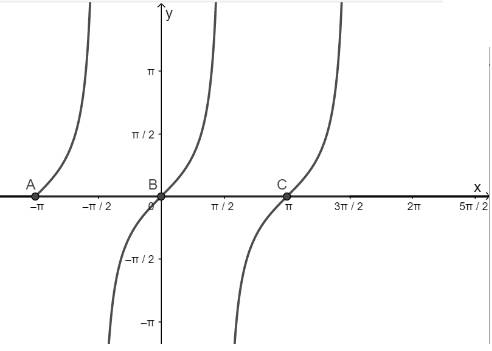
b) Hàm số y = tanx nhận giá trị bằng 0
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
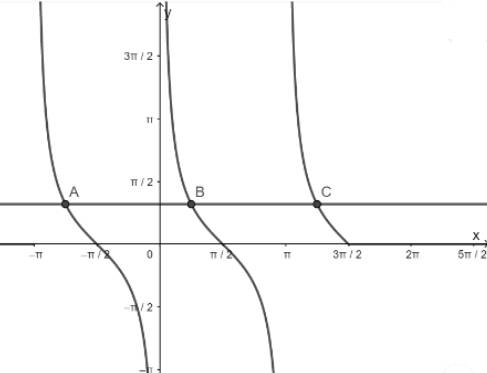
c) Hàm số y = cotx nhận giá trị bằng 1
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = cotx và y = 1
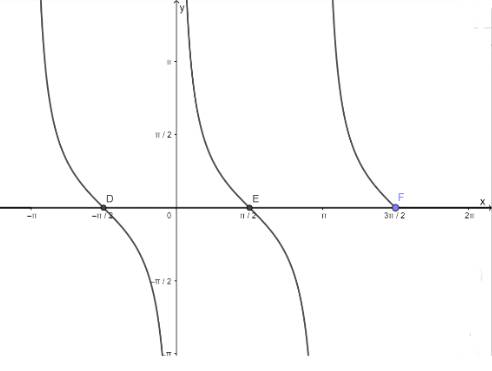
d) Hàm số y = cotx nhận giá trị bằng 0
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0

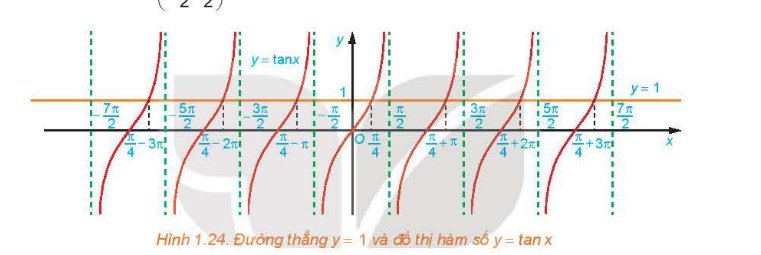
Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].
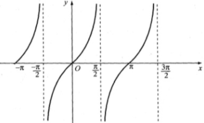
a. tan x = 0 tại các giá trị x = -π; 0; π.
(Các điểm trục hoành cắt đồ thị hàm số y = tanx).
b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.
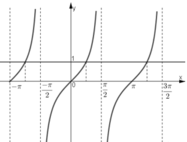
c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).
(Quan sát hình dưới)
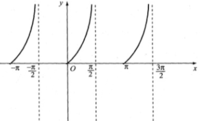
d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)
(Quan sát hình dưới).
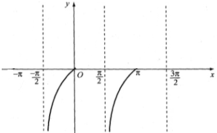

Đồ thị hàm số y = sin x:
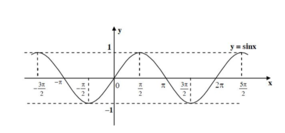
Dựa vào đồ thị hàm số y = sin x ta thấy
y = sin x > 0
⇔ x ∈ (-2π; -π) ∪ (0; π) ∪ (2π; 3π) ∪…
hay x ∈ (k2π; π + k2π) với k ∈ Z.

Bài 1. a) trục hoành cắt đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn
) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn ![]() chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
b) Đường thẳng y = 1 cắt đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) tại ba điểm có hoành độ
) tại ba điểm có hoành độ ![]() . Do đó trên đoạn
. Do đó trên đoạn ![]() chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là
chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là ![]() .
.
c) Phần phía trên trục hoành của đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng
) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng ![]() . Vậy trên đoạn
. Vậy trên đoạn ![]() , các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈
, các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈ ![]() .
.
d) Phần phía dưới trục hoành của đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng
) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng ![]() . Vậy trên đoạn
. Vậy trên đoạn ![]() , các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈
, các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈ ![]() .
.
a) \(\left\{-\pi;0;\pi\right\}\)
b) \(\left\{\dfrac{\pi}{4};\dfrac{\pi}{4}\pm\pi\right\}\)
c) \(\left(-\pi;-\dfrac{\pi}{2}\right)\cup\left(0;\dfrac{\pi}{2}\right)\cup\left(\pi;\dfrac{3\pi}{2}\right)\)
d) \(\left(-\dfrac{\pi}{2};0\right)\cup\left(\dfrac{\pi}{2};\pi\right)\)

Xét đồ thị hàm số y = sin x trên 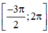 :
:
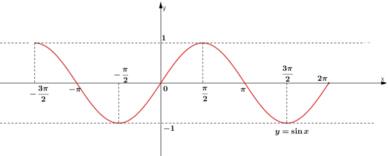
a. sin x = -1 ⇔ 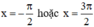
(Hoành độ giao điểm của đồ thị hàm số và đường thẳng y = -1).
b. sin x < 0
⇔ x ∈ (-π; 0) ∪ (π; 2π)
(Các khoảng mà đồ thị nằm phía dưới trục hoành).

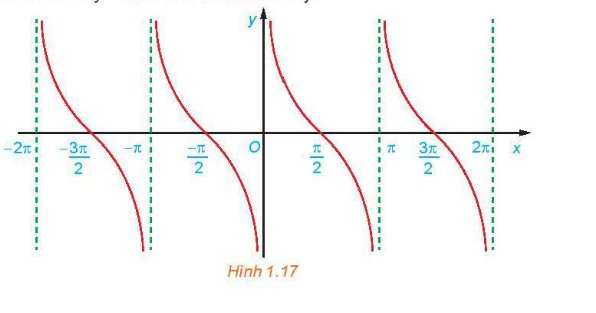
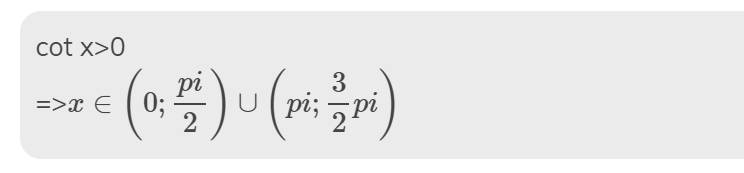
cot x>0
=>\(x\in\left(0;\dfrac{pi}{2}\right)\cup\left(pi;\dfrac{3}{2}pi\right)\)