
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2A=1+\dfrac{1}{2}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}\)
\(2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{18}+\dfrac{1}{32}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}+\dfrac{1}{64}\right)\)
\(A=1-\dfrac{1}{64}\)
\(A=\dfrac{63}{64}\)
giúp em với ạ , em cấn gấp , 4h em học rồi ạ . Cảm ơn những ai giúp em ạ , em tick luôn ạ

Đặt \(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(2A-A=\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\right)-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)\)
\(A=1-\frac{1}{64}\)
\(A=\frac{63}{64}\)
=32/64+14/64+8/64+4/64+2/64+1/64
=32+14+8+4+2+1/64
=61/64

\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{16}+\frac{1}{16}-\frac{1}{32}+\frac{1}{32}-\frac{1}{64}\)
\(=1-\frac{1}{64}\)
\(=\frac{63}{64}\)

A x 2 = 1 + 1/2+1/4+1/8+1/16+1/32
A x 2 - A = (1 + 1/2+1/4+1/8+1/16+1/32 ) - ( 1/2+1/4+1/8+1/16+1/32 +1/64)
A = 1 - 1/64
A = 63/64

b: A=1/3+1/9+...+1/3^10
=>3A=1+1/3+...+1/3^9
=>A*2=1-1/3^10=(3^10-1)/3^10
=>A=(3^10-1)/(2*3^10)
c: C=3/2+3/8+3/32+3/128+3/512
=>4C=6+3/2+...+3/128
=>3C=6-3/512
=>C=1023/512
d: A=1/2+...+1/256
=>2A=1+1/2+...+1/128
=>A=1-1/256=255/256

\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
đặt A = \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(A\cdot2=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(A\cdot2-A=\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)\) \(-\) \(\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\right)\)
\(A=\) \(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}-\frac{1}{64}-\frac{1}{128}\)
\(A=1-\frac{1}{128}\)
\(A=\frac{127}{128}\)
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
Ta lấy\(\frac{1}{128}\)là MSC. Ta tính được \(\frac{64}{128}+\frac{32}{128}+\frac{16}{128}+\frac{8}{128}+\frac{4}{128}+\frac{2}{128}+\frac{1}{128}\)
Kết quả bằng \(\frac{127}{128}\)

1/2 + 1/4 + 1/8 + 1/16 +1/32 + 1/64 + 1/128
=1-1/2+1/2-1/4+1/4-1/8+...+1/64+1/128
=1-1/128
=127/128

\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+...+\frac{1}{64}-\frac{1}{128}\)
\(=1-\frac{1}{128}\)
\(=\frac{127}{128}\)
A=\(\frac{1}{2}\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)=\frac{1}{2}\left(1+A-\frac{1}{2}-\frac{1}{128}\right)\)
2A=\(A+\frac{1}{2}-\frac{1}{128}=A+\frac{63}{128}\)
=> A=\(\frac{63}{128}\)
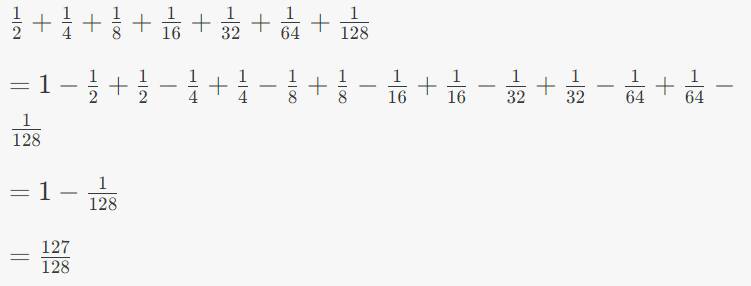
nhân hai lên rồi tính
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 = 1 - 1/2 + 1/2 - 1/4 + 1/4 - 1/8 + 1/8 + 1/16 + 1/16 - 1/32 + 1/32 - 1/64
Suy ra = 1 - 1/64
= 63/64