gọi lượng nước có trong dung dịch đầu tiền là x lít ; lượng axit có trong dung dịch đầu tiên là y lít ( x,y > 0 )

Sau khi thêm 1 lít axit vào dung dịch thì nồng độ của dung dịch là 40% nên ta có phương trình :

\(\frac{y+1}{x+y+1}=\frac{2}{5}\Leftrightarrow2x-3y=3\)( 1 )

Sau khi thêm vào dung dịch mới 1 lít nước thì nồng độ của dung dịch là \(33\frac{1}{3}\%\)nên ta có phương trình :

\(\frac{y+1}{x+y+2}=\frac{1}{3}\Leftrightarrow x-2y=1\)( 2 )

Từ ( 1 ) và ( 2 ) ta có HPT : \(\hept{\begin{cases}2x-3y=3\\x-2y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\y=1\end{cases}}\)

Vậy nồng độ axit trong dung dịch đầu tiền là : \(\frac{x}{x+y}.100\%=\frac{1}{1+3}.100\%=25\%\)

Gọi trọng lượng nước trong dung dịch trước khi đổ thêm nước là: x (g) (x > 0)

Vậy trước khi đổ thêm nước, trong dung dịch có 160g nước.

Kiến thức áp dụng

Để giải bài toán bằng cách lập phương trình ta làm theo các bước:

Bước 1: Lập phương trình

   + Chọn ẩn và đặt điều kiện cho ẩn

   + Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.

   + Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình

Bước 3: Đối chiếu điều kiện rồi kết luận.

Gọi trọng lượng nước trong dung dịch trước khi đổ thêm nước là: x (g) (x > 0)

Nồng độ muối của dung dịch khi đó là:  40 x + 40

Đổ thêm 200g nước vào dung dịch thì trọng lượng của dung dịch sẽ là: x+40+200(g)

Nồng độ của dung dịch bây giờ là: 40 x + 240

Vì nồng độ muối giảm 10% nên ta có có phương trình:  40 x + 40 - 40 x + 240 = 10 100

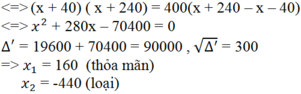
Vậy trước khi đổ thêm nước, trong dung dịch có 160g nước.