Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Xác suất chọn hsg là:
$\frac{40}{100}.\frac{70}{100}+\frac{20}{100}.\frac{30}{100}=\frac{17}{50}$
b.
Chọn ngẫu nhiên 3 hs, có $C^3_{100}$ cách chọn
Số hsg là: $(\frac{40}{100}.\frac{70}{100}+\frac{20}{100}.\frac{30}{100}).100=34$ (hs)
Chọn ngẫu nhiên được 2 hsg có $C^2_{34}C^1_{100-34}=C^2_{34}.C^1_{66}$ cách chọn
Xác suất cần tìm: $p=\frac{C^2_{34}.C^1_{66}}{C^3_{100}}=\frac{561}{2450}$

Đáp án A
Với mỗi câu hỏi, thí sinh có 4 phương án lựa chọn nên số phần tử của không gian mẫu là
n Ω = 4 10
Gọi X là biến cố “thí sinh đó đạt từ 8,0 điểm trở lên”
TH1. Thí sinh đó làm được 8 câu ( tức là 8,0 điểm):
Chọn 8 câu trong số 10 câu hỏi và 2 câu còn lại mỗi câu có 3 cách lựa chọn
đáp án sai nên có C 10 8 . 3 2 cách để thí sinh đúng 8 câu
TH2. Thí sinh đó làm được 9 câu (tức là 9,0 điểm)
Chọn 9 câu trong số 10 câu hỏi
và câu còn lại có 3 cách lựa chọn đáp án sai
nên có C 10 9 . 3 1 cách để thí sinh đúng 9 câu
TH3. Thí sinh đó làm được 10 câu (tức là 10,0 điểm)
Chỉ có 1 cách duy nhất.
Suy ra số kết quả thuận lợi cho biến cố X là
![]()
Vậy xác suất cần tìm là
P = n ( X ) n ( Ω ) = 436 4 10

Đáp án A
Với mỗi câu hỏi, thí sinh có 4 phương án lựa chọn nên số phần tử của không gian mẫu là ![]()
Gọi X là biến cố “thí sinh đó đạt từ 8,0 điểm trở lên”
TH1. Thí sinh đó làm được 8 câu (tức là 8,0 điểm): Chọn 8 câu trong số 10 câu hỏi và 2 câu còn lại mỗi câu có 3 cách chọn đáp án sai nên có ![]() cách để thí sinh đúng 8 câu.
cách để thí sinh đúng 8 câu.
TH2. Thí sinh đó làm được 9 câu (tức là 9,0 điểm): Chọn 9 câu trong số 10 câu hỏi và câu còn lại có 3 cách lựa chọn đáp án sai nên có ![]() cách để thí sinh đúng 9 câu.
cách để thí sinh đúng 9 câu.
TH3. Thí sinh đó làm được 10 câu (tức là 10,0 điểm): Chỉ có 1 cách duy nhất .
Suy ra số kết quả thuận lợi cho biến cố X là
![]()
Vậy xác suất cần tìm là
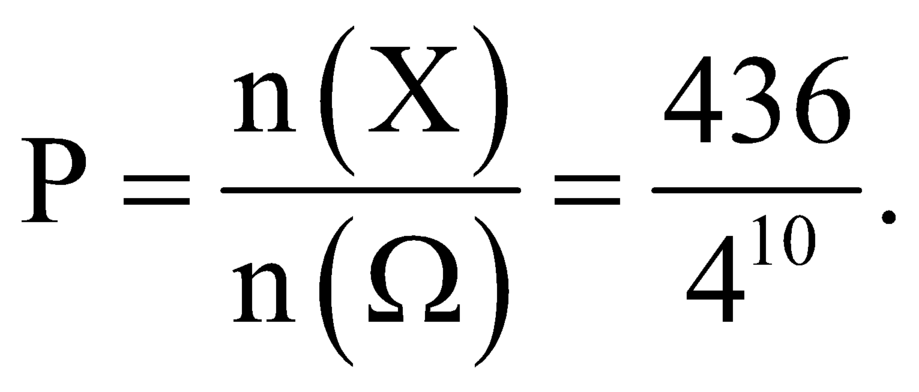

Trong không gian mẫu \(\Omega\) là tập hợp gồm tất cả các cặp hai bộ 3 câu hỏi, mà ở vị trí thứ nhất của cặp là bộ 3 câu hỏi thí sinh A chọn và ở vị trí thứ hai của cặp là bộ 3 câu hỏi thí sinh B chọn
Vì A cũng như B đều có \(C_{10}^3\) cách chọn 3 câu hỏi tứ 10 câu hỏi thí sinh nên theo quy tắc nhân ta có \(n\left(\Omega\right)=\left(C_{10}^3\right)^2\)
Kí hiệu X là biến cố " bộ 3 câu hỏi A chọn và bộ 3 câu hỏi B chọn là giống nhau"
Vì mỗi cách chọn 3 câu hỏi của A, B chỉ có duy nhất cách chọn 3 câu hỏi giống như A nên \(n\left(\Omega_X\right)=C_{10}^3.1=C_{10}^3\)
Vì vậy \(P\left(X\right)=\frac{n\left(\Omega_X\right)}{n\left(\Omega\right)}=\frac{C^3_{10}}{\left(C^3_{10}\right)^2}=\frac{1}{C^3_{10}}=\frac{1}{120}\)

