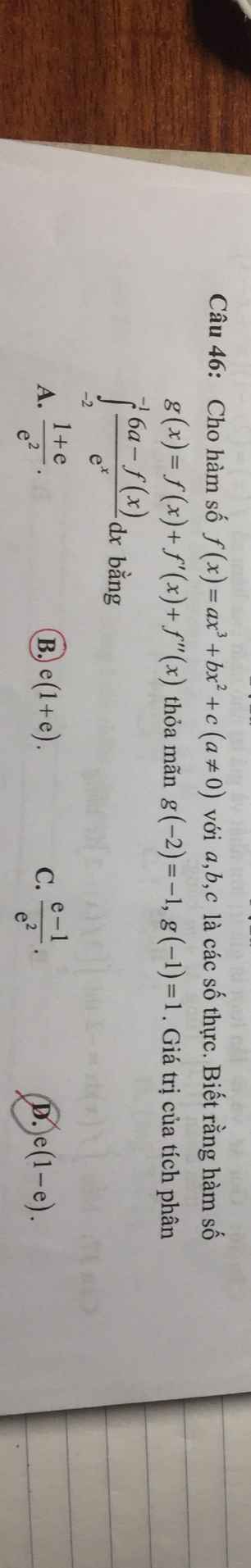hỏi chấm 

linh xem ở https://www.baogialai.com.vn/channel/12376/201909/neu-dang-buong-loi-phai-nhat-loi-dan-cua-bac-thi-se-gap-kho-khan-5647921/

Lời giải:

Giả sử \(A=(a,0,0); B=(0,b,0); C=(0,0,c)\)

Phương trình mặt phẳng $(P)$ là:

\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) (đây là dạng PTMP theo đoạn chắn rất quen thuộc)

Vì \(M\in (P)\Rightarrow \frac{1}{a}+\frac{2}{b}+\frac{1}{c}=1(*)\)

Ta có:

\(A=\frac{1}{OA^2}+\frac{1}{OB^2}+\frac{1}{OC^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)

Áp dụng BĐT Bunhiacopxky có:

\(\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)(1+2^2+1)\geq \left(\frac{1}{a}+\frac{2}{b}+\frac{1}{c}\right)^2\)

\(\Leftrightarrow 6A\geq 1\Leftrightarrow A\geq \frac{1}{6}\). Điểm "min" xảy ra khi : \(\frac{1}{a}=\frac{1}{2b}=\frac{1}{c}\)

Đặt \(\frac{1}{a}=\frac{1}{2b}=\frac{1}{c}=t\Rightarrow \left\{\begin{matrix} a=\frac{1}{t}\\ b=\frac{1}{2t}\\ c=\frac{1}{t}\end{matrix}\right.\). Thay vào \((*)\Rightarrow t=\frac{1}{6}\)

Thay vào ptmp ban đầu suy ra ptmp (P) là:

\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\Leftrightarrow xt+2yt+zt=1\)

\(\Leftrightarrow \frac{x}{6}+\frac{y}{3}+\frac{z}{6}=1\) hay \(x+2y+z-6=0\)

\(I=\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx-\int\limits^{-1}_{-2}\dfrac{f\left(x\right)}{e^x}dx=J-I_1\)

Xét \(I_1\) , đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_1=-f\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f'\left(x\right)}{e^x}dx=-f\left(-1\right).e+f\left(-2\right).e^2+I_2\)

Xét \(I_2\) , đặt \(\left\{{}\begin{matrix}u=f'\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f''\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_2=-f'\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f''\left(x\right)}{e^x}dx=-f'\left(-1\right).e+f'\left(-2\right).e^2+I_3\)

Xét \(I_3\) , đặt \(\left\{{}\begin{matrix}u=f''\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'''\left(x\right)dx=6a.dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_3=-f''\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx=-f''\left(-1\right).e+f''\left(-2\right).e^2+J\)

Do đó:

\(I=J+f\left(-1\right).e-f\left(-2\right).e^2+f'\left(-1\right).e-f'\left(-2\right).e^2+f''\left(-1\right).e-f''\left(-2\right).e^2-J\)

\(=e\left[f\left(-1\right)+f'\left(-1\right)+f''\left(-1\right)\right]-e^2\left[f\left(-2\right)+f'\left(-2\right)+f''\left(-2\right)\right]\)

\(=e.g\left(-1\right)-e^2.g\left(-2\right)=e+e^2=e\left(e+1\right)\)

Bài 1:

Gọi tọa độ của \(A=(0,0,a)\) và \(B=(m,n,p)\)

Vì $(P)$ vuông góc với $(d)$ nên \(\overrightarrow {n_P}=\overrightarrow {u_d}=(2,-1,1)\) kết hợp với $(P)$ chứa $A$ nên PTMP: \((P):2x-y+z-a=0\)

Ta có \(B\in (P)\Rightarrow 2m-n+p-a=0(1)\)

Mặt khác \(B\in (d')\Rightarrow \frac{m-1}{1}=\frac{n}{2}=\frac{p+2}{1}=t\Rightarrow \left\{\begin{matrix} m=t+1\\ n=2t\\ p=t-2\end{matrix}\right.\)

Thay vào $(1)$ ta thu được $t=a$

\(\Rightarrow AB=\sqrt{m^2+n^2+(p-a)^2}=\sqrt{(a+1)^2+(2a)^2+4}=\sqrt{5a^2+2a+5}\geq \frac{2\sqrt{30}}{5}\Leftrightarrow a=\frac{-1}{5}\)

Có nghĩa là để $AB$ min thì $a=\frac{-1}{5}$

Vậy PTMP: \(2x-y+z-\frac{1}{5}=0\)

Câu 2:

Thay toạ độ $A$ và $B$ vào $(P)$ có \([3.1-4(-1)+2-1](3.3-4.0+1-1)>0\) nên $A,B$ cùng phía so với $(P)$

Lấy $A'$ đối xứng với $A$ qua $(P)$ \(\Rightarrow MA=MA'\Rightarrow MA+MB=MA'+MB\geq A'B\)

Do đó \((MA+MB)_{\min}\Leftrightarrow A',M,B\) thẳng hàng

Biểu thị $(d)$ là đường thẳng chứa đoạn $AA'$.

Hiển nhiên \((d)\perp (P)\Rightarrow \overrightarrow{u_d}=\overrightarrow {n_P}=(3,-4,1)\)

Kết hợp với $A\in (d)$ nên \(d:\frac{x-1}{3}=\frac{y+1}{-4}=\frac{z-2}{1}=t\)

Khi đó gọi \(H\equiv AA'\cap (P)\). Dễ có \(H=(\frac{1}{13},\frac{3}{13},\frac{22}{13})\)

Lại có $H$ là trung điểm của $AA'$ nên tọa độ của $A'$ là

\(\left\{\begin{matrix} x_{A'}=2x_H-x_A=\frac{-11}{13}\\ y_{A'}=2y_H-y_A=\frac{19}{13}\\ z_{A'}=2z_H-z_A=\frac{18}{13}\end{matrix}\right.\)

Khi đó ta dễ dàng viết được PTĐT chứa $A'B$ là \(\frac{13(x-3)}{50}=\frac{13y}{19}=\frac{13(z-1)}{5}\)

Tọa độ của $M$ là nghiệm của hệ

\(\left\{\begin{matrix} \frac{13(x-3)}{50}=\frac{13y}{19}=\frac{13(z-1)}{5}\\ 3x-4y+z-1=0\end{matrix}\right.\Rightarrow M(\frac{-213}{79},\frac{-171}{79},\frac{34}{79})\)

.

Vì một tuần thì có 7 ngày, hay nói cách khác, một tuần có chu kỳ 7. Cứ hết 7 ngày từ thứ Hai đến Chủ Nhật thì lại quay về bắt đầu của chu kỳ 7 ngày khác. Cũng giống như từ 1 đến 10 là một chu kỳ 10 vậy.

Tính chất hàm đặc trưng

Nếu \(f\left(x\right)\) đơn điệu thì \(f\left(x_1\right)=f\left(x_2\right)\Leftrightarrow x_1=x_2\)

Ở đây \(f\left(t\right)=e^t+t\) đơn điệu nên \(f\left(t_1\right)=f\left(t_2\right)\Leftrightarrow t_1=t_2\)

Trong đó \(\left\{{}\begin{matrix}t_1=m.cosx-sinx\\t_2=2\left(1-sinx\right)\end{matrix}\right.\)

   1+1=2vì chúng ta  có 1cái người khác cho mình  thêm  1cái sẽ=2                                                                                                                                           => 1+1=2

I. Nội qui tham gia "Giúp tôi giải toán"

1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;

2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.

3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.

Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

\(y'=\dfrac{-3}{\left(x-2\right)^2}\)

d. Phương trình hoành độ giao điểm

\(\dfrac{x+1}{x-2}=x-\dfrac{1}{2}\Leftrightarrow2x^2-7x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{2}\end{matrix}\right.\)

Tại \(x=0\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{3}{4}\\y=-\dfrac{1}{2}\end{matrix}\right.\) 

Pttt: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)

Tại \(x=\dfrac{7}{2}\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{4}{3}\\y=3\end{matrix}\right.\) tiếp tuyến: \(y=-\dfrac{4}{3}\left(x-\dfrac{7}{2}\right)+3\)

e.

Tam giác ABC là tam giác nào nhỉ? Có lẽ đó là tam giác OAB?

g.

Giao điểm (C) với Ox có tọa độ \(\left(-1;0\right)\)

\(\Rightarrow y'\left(-1\right)=-\dfrac{1}{3}\)

Phương trình tiếp tuyến:

\(y=-\dfrac{1}{3}\left(x+1\right)\)

h.

Giao điểm (C) với Oy có tọa độ \(\left(0;-\dfrac{1}{2}\right)\)

Chính là trường hợp đầu của câu d, phương trình: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)