
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) để ΔABC cân tại C thì AC=BC hay AC2=BC2
mà AC2=(6-3a)2+(a-3)2 BC2=(3-3a)2+(a-2)2
=======>(6-3a)2+(a-3)2=(3-3a)2+(a-2)2
<=> a=8/5======>C(1/5,8/5)
2)ΔABD vuông tại A thì
\(\overrightarrow{AB}\) x \(\overrightarrow{AD}\)=0 do D thuộcΔ nen D(5-3b,b)
\(\overrightarrow{AB}\)=(3,-1)
\(\overrightarrow{AD}\)=(6-3b,b-3)========>3x(6-3b)-1x(b-3)=0
<=>b=21/10=========>D(-13/10,21/10)

Chọn A
Chuyển d về phương trình thám số, gọi tọa độ điểm M theo tham số t. Tìm t từ điều kiện vuông góc, M A → . M B → = 0

Ta đã biết 1 góc bù có 2 cạnh tạo thành 1 góc bẹt = 180 độ mà 2 góc kề bù thì chắc chắn 2 tía nằm 2 phía đối nhau mà 1 tia nằm trên mà tia phân giác tạo với 2 canh 2 góc bằng nhau nên 2 góc đó sẽ có sổ đo là 180 x 1/2 = 90 độ mà 90 độ là góc vuông ![]()

Chọn đáp án B
Ta có y ' = 3 x 2 - 11 . Giả sử M m ; m 3 - 11 m thì tiếp tuyến ∆ của (C) tại điểm M có hệ số góc là k = y ' m = 3 m 2 - 11
Phương trình ∆ : y = 3 m 2 - 11 x - 2 m .
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng ∆ là:
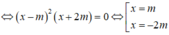
Suy ra hoành độ các điểm Mn lập thành một cấp số nhân (xn) có số hạng đầu x 1 = - 2 và công bội q = -2.
Ta có x n = x 1 . q n - 1 = - 2 n
![]() .
.
Để 11 x n + y n + 2 2019 = 0
⇔ 3 n = 2019 ⇔ n = 673

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

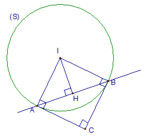
mặt cầu tâm I, bán kính R = 2.
Giao của tiếp diện với là A, B và là điểm C.
Tiếp diện của (S) tại A và B vuông góc với nhau ⇔ IACB là hình vuông
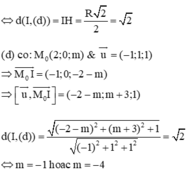
Chọn B
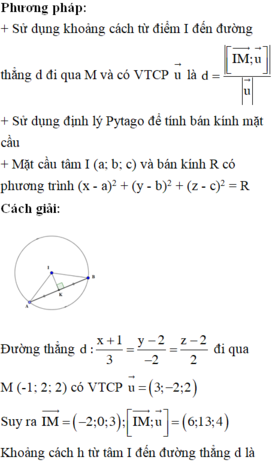

Bằng 3 mà??
Vì nó là 1 phép tính đúng?