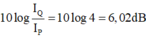Đáp án D

+ Khi xác định mức cường độ âm di chuyển từ M đến N thì thu được mức cường độ âm lớn nhất tại I với I là đường vuông góc hạ từ O xuống MN.

→ Áp dụng hệ thức lượng trong tam giác vuông ta tìm được MI = 6 cm.

O I = 6 3   c m .

+ Mức cường độ âm tại I:

L I = L M + 20 log OM IM = 60 + 20 log 12 6 3 = 61 , 25   dB .

+ Thời gian để thiết bị chuyển động từ M đến I:

t = 2 MI a = 2 . 6 3 = 2   s .

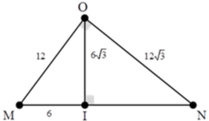
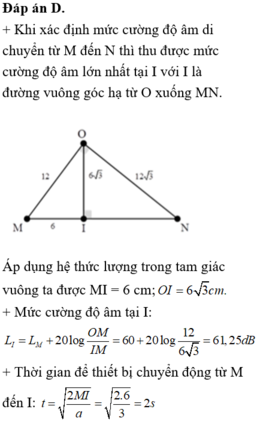
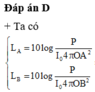
+ Ta có: L_N - L_M = 20 dB →   10 log P 4 π O N 2 . I 0   -   10 log P 4 π O M 2 . I 0   =   20  

→ O M O N   = 10   → OM = 100 m → MN = 90 m.

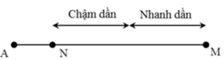
+ Vì thiết bị chuyển động với 2 giai đoạn nên ta có thể coi một giai đoạn chuyển động nhanh dần đều với a = 0,4 m/s² và một giai đoạn chuyển động chậm dần đều với gia tốc 0,4 m/s² đến khi dừng lại tại N.

* Giai đoạn 1 ta có: v² - 0 = 2as₁ → s 1   =   v 2 2 a  

* Giai đoạn 2 ta có: 0 - v² = -2as₂ → s 2   =   v 2 2 a

Mà s₁ + s₂ = MN = 90 m  → v = 6 m/s.

+ v = 0 + at₁  → t₁ = 15 s

+ 0 = v - at₂  → t₂ = 15 s

→ t = 30 s gần với giá trị của đáp án B nhất.

Đáp án B

Đáp án D

+ Ta có:

L N - L M = 20 log ( OM ON ) ⇒ OM = 10 ON

Vậy MN = 135 m

Xe chuyển động thành hai giai đoạn trên MN, nửa giai đoạn đầu là nhanh dần đều, nửa giai đoạn sau là chậm dần đều

→ t = 2 MN 2 a = 2 135 2 . 3 , 75 = 8 , 48   s .

Đáp án B

Mức cường độ âm tại A,B bằng nhau nên OA = OB . Mức cường độ âm tại C cực đại nên C là trung điểm của AB

Đáp án B

Vì mức cường độ âm tại A và B bằng nhau nên suy ra OA = OB. C có mức cđ âm max nên C gần O nhất, hay OC vuông góc với AB.

Có P 4 π O A 2 = I 0 .10 L P 4 π O C 2 = I 0 .10 L m ax ⇒ 10 L max − L = O A O C 2 ⇒ 10 0 , 3 = O A O C 2 ⇒ O C = 2 , 1238 ( m )

⇒ A B = 2 A C = 2 O A 2 − O C 2 ≈ 4 , 2376 ( m ) ⇒ t = A B v = 3 , 5313 ( s )

Câu hỏi này bạn cần biết phân tích chuyển động biến đổi đều của xe, quãng đường xe chuyển động và âm chuyển động để giải bài toán.

+ Biết mức cường độ âm tại N lớn hơn mức cường độ âm tại M là 20 dB, ta có:

\({{L}_{N}}-{{L}_{M}}=10.\lg{{\left( \dfrac{{{R}_{M}}}{{{R}_{N}}} \right)}^{2}}=20\Rightarrow {{R}_{M}}=OM=10{{R}_{N}}=100m\)

\(\Rightarrow MN = OM – ON = 90 m\)

Vật (thiết bị) đi từ M nhanh dần đều đến trung điểm của MN, sau đó chuyển động chậm dần và dừng lại tại N, nên ta có: \({{t}_{MN}}=2.{{t}_{MC}}\)(C là trung điểm của MN)
\(MC=\dfrac{MN}{2}=\dfrac{1}{2}at_{MC}^{2}\Rightarrow {{t}_{MC}}=\sqrt{\dfrac{MN}{a}}\)
\(\Rightarrow t={{t}_{MN}}=2\sqrt{\dfrac{MN}{a}}=2\sqrt{\dfrac{90}{04}}=30s\)

Vậy giá trị gần nhất là 32s

Đáp án B

Ta có mức cường độ âm:

L = 10 . log I I 0 = 10 log P 4 πR 2 . I 0 ⇒ L max ⇔ R min

(với R là khoảng cách từ nguồn âm đến điểm khảo sát)

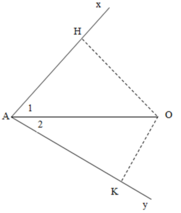
Gọi H và K là chân đường vuông góc hạ từ O xuống Ax và Ay.

=> Khi đi theo hướng Ax, mức cường độ âm lớn nhất người đó đo được khi người đó đứng tại H. Khi đi theo hướng Ay, mức cường độ âm lớn nhất người đó đo được khi người đó đứng tại K.

Ta   có : L A = 10 log P 4 π . OA 2 . I 0 = 50 L H = 10 log P 4 π . OH 2 . I 0 = 57 L K = 10 log P 4 π . OK 2 . I 0 = 62

⇒ L H - L A = 10 . log OA 2 OH 2 = 7 ⇒ OA = 2 , 2387 OH L K - L A = 10 . log OA 2 OK 2 = 12 ⇒ OA = 3 , 981 OK

sin A 1 = O H O A = O H 2 , 2387 O H = 1 2 , 2387 ⇒ A 1 ^ = 26 , 53 0

sin A 2 = O K O A = O K 3 , 981 O K = 1 3 , 981 ⇒ A 2 ^ = 14 , 55 0

⇒ xAy ^ = A 1 ^ + A 2 ^ = 41 0