Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

kẻ 1 đường thẳng vuông góc với BC cắt AC ở E
Xét tam giác CBE vuông tại B có:
1/BK^2=1/BC^2+1/BE^2 (hệ thức lượng)(1)
ta lại có:
*AH vuông góc với BC
BE vuông góc với BC
=>AH//BE (2)
*tam giác ABC cân tại A có:
AH là đường cao của tam gic1 ABC nên:
AH cũng là đường trung tuyến của tam giác ABC
=>H là trung điểm của BC (3)
từ (2) và (3) suy ra:
A là trung điểm của CE (4)
từ (3) và (4) suy ra:
AH là đường trung bình của tam giác CBE
=> AH=BE/2
=>BE=2AH
=>BE2=4AH2 (5)
từ (1) và (5) suy ra:
1/BK^2=1/BC^2+1/4AH^2

a) Do AH là đường cao trong tam giác ABC cân tại A
\(\Rightarrow\) AH cũng là đường trung tuyến trong tam giác ABC
Suy ra H là trung điểm của BC.
mà AH//BD (vì cùng vuông góc với BC)
\(\Rightarrow\) AH là đường trung bình của tam giác DBC
\(\Rightarrow\) 2AH=BD
b)Áp dụng hệ thức trong tam giác vuông có
\(\dfrac{1}{BK^2}=\dfrac{1}{BD^2}+\dfrac{1}{BC^2}=\dfrac{1}{\left(2AH\right)^2}+\dfrac{1}{BC^2}\) \(=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)
Vậy...

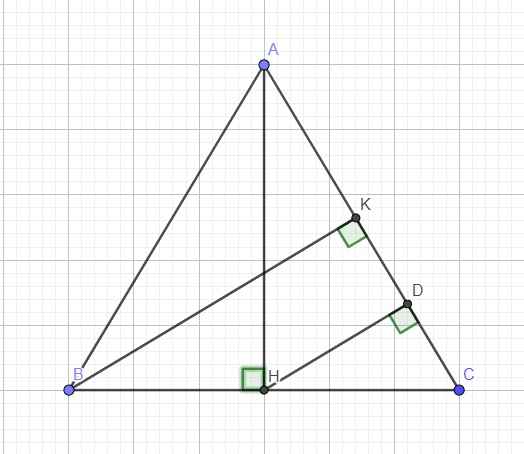
Từ H kẻ \(HD\perp AC\Rightarrow HD||BK\) (cùng vuông góc AC)
Mà ABC cân tại A \(\Rightarrow\) H là trung điểm BC \(\Rightarrow HC=\dfrac{BC}{2}\)
\(\Rightarrow\) HD là đường trung bình tam giác BCK
\(\Rightarrow HD=\dfrac{BK}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao HD ứng với cạnh huyền:
\(\dfrac{1}{HD^2}=\dfrac{1}{AH^2}+\dfrac{1}{CH^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{BK}{2}\right)^2}=\dfrac{1}{AH^2}+\dfrac{1}{\left(\dfrac{BC}{2}\right)^2}\)
\(\Leftrightarrow\dfrac{4}{BK^2}=\dfrac{1}{AH^2}+\dfrac{4}{BC^2}\)
\(\Leftrightarrow\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

Lấy E sao cho A là trung điểm của CE
Xét ΔEBC có
BA là đường trung tuyến
BA=CE/2
Do đó: ΔEBC vuông tại E
Xét ΔCBE có AH//BE
nên AH/BE=CH/CB=1/2
=>AH=1/2BE
Xét ΔBEC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BE^2}\)
=>\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)