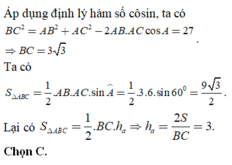
Ta có A H → = a + 3 ; b  ;   B C → = − 1 ; 6 B H → = a − 3 ; b  ;  A C → = 5 ; 6 .  

Từ giả thiết, ta có:

               A H → . B C → = 0 B H → . A C → = 0 ⇔ a + 3 . − 1 + b .6 = 0 a − 3 .5 + b .6 = 0 ⇔ a = 2 b = 5 6 ⇒ a + 6 b = 7.

 Chọn C.

Ta có A H → = a + 3 ; b  ;   B C → = − 1 ; 6 B H → = a − 3 ; b  ;  A C → = 5 ; 6 .  

Từ giả thiết, H là trực tâm tam giác ABC nên ta có:

      A H → . B C → = 0 B H → . A C → = 0 ⇔ a + 3 . − 1 + b .6 = 0 a − 3 .5 + b .6 = 0 ⇔ a = 2 b = 5 6 ⇒ a + 6 b = 7.  

Chọn C.

a)

– Tọa độ trọng tâm G của tam giác ABC là:

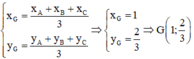
– Tọa độ trực tâm H của tam giác ABC:

Cách 1:

+ Phương trình đường cao BD:

BD ⊥ AC ⇒ Đường thẳng BD nhận 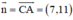 là một vtpt

BD đi qua B(2; 7)

⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0

+ Phương trình đường cao CE:

CE ⊥ AB ⇒ Đường thẳng CE nhận 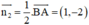 là một vtpt

CE đi qua C(–3; –8)

⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.

Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:

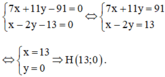
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC

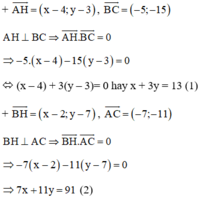
Từ (1) và (2) ta có hệ phương trình

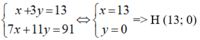
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC

Khi đó TA = TB = TC = R.

+ TA = TB ⇒ AT2 = BT2

⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2

⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49

⇒ 4x – 8y = –28

⇒ x – 2y = –7 (1)

+ TB = TC ⇒ TB2 = TC2

⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2

⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64

⇒ 10x + 30y = –20

⇒ x + 3y = –2 (2)

Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).

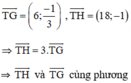
⇒ T, H, G thẳng hàng.

c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)

Bán kính đường tròn ngoại tiếp ΔABC:

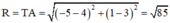
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:

(x + 5)2 + (y – 1)2 = 85

a: \(\overrightarrow{AB}=\left(-11;11\right);\overrightarrow{AC}=\left(-2;6\right)\)

Vì -11/-2<>11/6

nên A,B,C thẳng hàng

ABCD là hình bình hành

=>vecto DC=vecto AB

=>5-x=-11 và 4-y=11

=>x=16 và y=-7

b: \(\overrightarrow{BH}=\left(x+4;y-9\right)\); vecto BC=(9;-5); vecto AH=(x-7;y+2)

Theo đề, ta có: 

(x+4)/9=(y-9)/-5 và 9(x-7)+(-5)(y+2)=0

=>-5x-20=9y-81 và 9x-63-5y-10=0

=>-5x-9y=-61 và 9x-5y=73

=>x=481/53; y=92/53

c: Vì (d') vuông góc (d) nên (d'): 4x+3y+c=0

Thay x=-2 và y=3 vào (d'), ta được:

c+4*(-2)+3*3=0

=>c=-1

1.2

a.

\(\overrightarrow{AB}=\left(4;-2\right)=2\left(2;-1\right)\Rightarrow\) đường thẳng AB nhận (1;2) là 1 vtpt

Phương trình đường thẳng AB:

\(1\left(x+1\right)+2\left(y-4\right)=0\Leftrightarrow x+2y-7=0\)

b.

Gọi M là trung điểm AB \(\Rightarrow M\left(1;3\right)\)

\(AB=\sqrt{4^2+\left(-2\right)^2}=2\sqrt{5}\) \(\Rightarrow AM=\dfrac{1}{2}AB=\sqrt{5}\)

Đường tròn đường kính AB có tâm M và bán kính \(R=AM=\sqrt{5}\) nên có pt:

\(\left(x-1\right)^2+\left(y-3\right)^2=5\)

1.1

a. \(\overrightarrow{CB}=\left(5;15\right)=5\left(1;3\right)\) ; \(\overrightarrow{CA}=\left(7;11\right)\)

Đường cao qua A vuông góc BC nên nhận (1;3) là 1 vtpt

Phương trình đường cao đi qua A có dạng:

\(1\left(x-4\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-13=0\)

Đường cao qua B vuông góc AC nhận (7;11) là 1 vtpt có dạng

\(7\left(x-2\right)+11\left(y-7\right)=0\Leftrightarrow7x+11y-91=0\)

Trực tâm H là giao điểm 2 đường cao nên tọa độ thỏa mãn:

\(\left\{{}\begin{matrix}x+3y-13=0\\7x+11y-91=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=13\\y=0\end{matrix}\right.\)

\(\Rightarrow H\left(13;0\right)\)

\(\overrightarrow{BC}=\left(2;4\right)=2\left(1;2\right)\)

Do đường cao AH vuông góc BC nên nhận \(\left(1;2\right)\) là 1 vtpt

Phương trình AH qua A có dạng:

\(1\left(x-2\right)+2\left(y-1\right)=0\Leftrightarrow x+2y-4=0\)

$\overrightarrow{BC}=\left(1;2\right)$

AH $\left(1;2\right)$ => vtpt

Phương trình AH qua A có dạng: 

$1\left(x-2\right)+2\left(y-1\right)=0\iff x+2y-4=0$

a: vecto AB=(-7;1)

vecto AC=(1;-3)

vecto BC=(8;-4)

b: \(AB=\sqrt{\left(-7\right)^2+1^2}=5\sqrt{2}\)

\(AC=\sqrt{1^2+\left(-3\right)^2}=\sqrt{10}\)

\(BC=\sqrt{8^2+\left(-4\right)^2}=\sqrt{80}=4\sqrt{5}\)