Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AE là đường phân giác của tam giác ABC nên
=
Áp dụng tính chất tỉ lệ thức
= = =
=> EB = =
EC = BC- BE ≈ 3,8

AE là phân giác BAC
=> \(\frac{EB}{EC}=\frac{AB}{AC}=\frac{5}{6}\)
=> \(\frac{EB}{5}=\frac{EC}{6}=\frac{EB+EC}{5+6}==\frac{BC}{11}=\frac{7}{11}\) ( Áp dụng dãy tỉ số bàng nhau )
=> EB = 7/11 . 5 = 35/11
=> EC = 7/11 . 6 = 42 / 11

Ta có: AE là phân giác góc BAC nên theo tính chất phân giác, ta có:
\(\frac{EB}{EC}=\frac{AB}{AC}=\frac{5}{6}\)
\(=>\frac{EB}{5}=\frac{EC}{6}=\frac{EB+EC}{5+6}=\frac{BC}{11}=\frac{7}{11}\)
\(=>EB=\frac{35}{11}\)
\(=>EC=\frac{42}{11}\)

Sửa đề: BC=5,5cm
Xet ΔABC có AE là phân giác
nên EB/AB=EC/AC
=>EB/5=EC/6=(EB+EC)/(5+6)=5,5/11=0,5
=>EB=2,5cm; EC=3cm

phuong trinh:
BE/BA=CE/CA(THEO TINH CHAT DUONG PHAN GIAC CUA TAM GIAC)
Hay BE/5=CE/7
Ap dung tinh chat cua day ti so bang nhau ta co:
BE/5=CE/7=(BE+CE)/5+7=BC/12=7/12
Tu BE/5=7/12=>BE=(7*5)/12=35/12
CE/7=7/12=>CE=(7*7)/12=49/12

a) Do AE là đường phân giác của ABC , nên :
\(\frac{AB}{AC}=\frac{BE}{EC}\)suy ra \(\frac{EC}{AC}=\frac{BE}{AB}\)
( tính chất của tỉ lệ thức )
Áp dụng tính chất của DTSBN , ta có :
\(\frac{EC}{AC}=\frac{BE}{AB}=\frac{EC+BE}{AC+AB}=\frac{BC}{6+5}=\frac{7}{11}\)
+) \(\frac{EC}{AC}=\frac{7}{11}\Rightarrow\frac{EC}{6}=\frac{7}{11}\)
\(\Rightarrow EC=\frac{6.7}{11}=\frac{42}{11}\)
+) \(EB=BC-EC=7-\frac{42}{11}=\frac{35}{11}\)
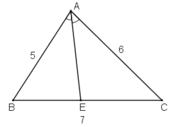

GIẢI.
Xét tam giác ABC, có : AE tia phân giác của góc BAC (gt)
=>\(\frac{EB}{EC}=\frac{AB}{AC}\) hay \(\frac{EB}{AB}=\frac{EC}{AC}\)
Áp dụng tính chất dãy tỉ lệ thức :
\(\frac{EB}{AB}=\frac{EC}{AC}=\frac{EB+EC}{AB+AC}=\frac{BC}{AB+AC}=\frac{7}{11}\)
=>EB =\(\frac{5.7}{11}\) =3,18cm.
=>EC =\(\frac{6.7}{11}\) =3,82cm.
AE là đường phân giác của tam giác ABC nên
\(\frac{AE}{AB}=\frac{EC}{AC}\)
Áp dụng tính chất tỉ lệ thức
\(\frac{AE}{AB}=\frac{EC}{AC}=\frac{EB+EC}{AB+AC}=\frac{BC}{AB+AC}\)
\(\Rightarrow EB=\frac{AB.BC}{AB+AC}=\frac{5.7}{5+6}\)
EC = BC- BE ≈ 3,8
- See more at: http://toanhocviet.com/tinh-chat-duong-phan-giac-cua-tam-giac_n59185_g790.aspx#sthash.odDjd4Z7.dpuf