Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: góc ECM+góc EDM=180 độ
=>ECMD nội tiếp
góc MNB=1/2*180=90 độ
EM vuông góc AB
MN vuông góc AB
=>E,M,N thẳng hàng
2: Đề bài yêu cầu gì?

a) nghe nói ông ra r nên thôi nhá
b) cm E là trung điểm AB (dễ nhá)
có AH//BD
=> cm đc FA/DM= CF/MC=FH/MB (Ta lét nhá)
có FA/DM=FH/MB và MD=MB (cm đc từ câu a)
=>FA=FH
=> F là trung điểm AH
=> FE là đường trung bình của tam giác AHB
=> EF//BC
c) cm AN/MN = FA/BM= HF/BM=CF/CM
tam giác MNC có : AN/MN=FC/MC
=> FA//CN
=> BD//NC (// FA)
=> góc HCN=90
cm HB/HC=FM/FC=MB/NC (talet và hệ quả talet)
xét 2 tam giác HBM vuông và HCN vuông: có HB/HC=BM/NC
=>đồng dạng
=> HM/HN=HB/HC
mà HB/HC=BF/FN=AM/AN
=>HM/HN=AM/AN
=>đpcm ( định lí đảo về đường phân giác gì gì đấy thì phải,ko nhớ rõ,ông tự tìm trong sách nhá =)) )
d) tính OA
cm OAM vuông tại A (tiếp tuyến nhá)
cm OEA đồng dạng với OAM (g.g)
=> OA/OM=OE/OA
=> tính đc OE,dựa vào tính chất đường trung bình cảu tam giác tính đc AC
có OE,OA=> tính đc AE=> tính đc AB
có AB,AC,BC => tính đc chu vi
Cho tam giác ABC vuông tại A, với AC<AB;AH là đường cao kẻ từ A.Các tiếp tuyến tại A và B với đ/tròn tâm O ngoại tiếp tam giác ABC cắt nhau tại M.Đoạn MO cắt AB tại E.Đoạn MC cắt đường cao AH tại F.Kéo dài CA cắt BM ở D.Đường thẳng BF cắt đường thẳng AM tại N.
a)C/M: OM//CD và M là trung điểm của BD
b)C/M: EF//BC
c)C/M: HA là tia p/g của góc MHN
d)Cho OM=BC=4cm.Tính chu vi tam giác ABC
Toán lớp 9
ai tích mình tích lại nh nha

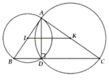
a, A D B ^ là góc nội tiếp trên đường kính AB => A D ⊥ B D
b, Do
A
D
C
^
=
90
0
nên DÎ đường tròn (k;
A
C
2
)
c, ∆IBD cân tại I có B ^ = 60 0 => ∆IBD đều => B I D ^ = 60 0
=> l B D ⏜ = π . 5 2 . 60 180 = 5 6 π cm

a: góc ADB=1/2*180=90 độ
góc EDF+góc EHF=180 độ
=>EDFH nội tiếp
b: gócBAE+góc CAE=90 độ
góc BEA+góc HAE=90 độ
mà góc CAE=góc HAE
nên góc BEA=góc BAE
=>ΔBAE cân tại B

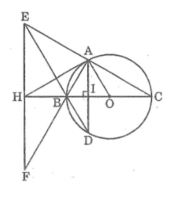
Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên: HA = HE = HF = (1/2).EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.
Đặt \(BC=x\left(x>5\right)\)
Trong đường tròn (O) có đường kính CD và \(N\in\left(O\right)\) nên \(\widehat{DNC}=90^o\) hay \(\widehat{BND}=90^o\)
Vì BD là tia phân giác của \(\widehat{ABC}\) nên \(\widehat{ABD}=\widehat{NBD}\)
Xét 2 tam giác ABD và NBD vuông tại A và N, có \(\widehat{ABD}=\widehat{NBD}\) và cạnh BD chung nên \(\Delta ABD=\Delta NBD\left(ch-gn\right)\)
\(\Rightarrow BA=BN=5\) \(\Rightarrow NC=BC-BN=5-x\)
Lại có \(\widehat{OMD}=\widehat{ODM}=\widehat{BDA}=\widehat{BDN}\) nên OM//ND (2 góc đồng vị bằng nhau)
Tam giác CND có O là trung điểm DC, OH//DN và \(H\in NC\) nên H là trung điểm NC \(\Rightarrow HC=\dfrac{NC}{2}=\dfrac{x-5}{2}\)
Theo định lý Pythagoras, có \(AC=\sqrt{BC^2-AB^2}=\sqrt{x^2-25}\)
Theo tính chất đường phân giác trong tam giác, ta có:
\(\dfrac{DA}{AB}=\dfrac{DC}{CB}=\dfrac{AC}{AB+CB}\) \(\Rightarrow\dfrac{DA}{5}=\dfrac{DC}{x}=\dfrac{\sqrt{x^2-25}}{x+5}\)
\(\Rightarrow DA=\dfrac{5\sqrt{x^2-5}}{x+5}\) và \(DC=\dfrac{x\sqrt{x^2-5}}{x+5}\)
\(\Rightarrow R_{\left(O\right)}=\dfrac{DC}{2}=\dfrac{x\sqrt{x^2-5}}{2x+10}\)
Lại có \(DN=AD=\dfrac{5\sqrt{x^2-5}}{x+5}\)
\(OH=\dfrac{DN}{2}=\dfrac{5\sqrt{x^2-25}}{2x+10}\) (OH là đường trung bình của tam giác CND)
\(\Rightarrow MH=MO+OH=\dfrac{x\sqrt{x^2-25}}{2x+10}+\dfrac{5\sqrt{x^2-25}}{2x+10}\) \(=\dfrac{\sqrt{x^2-25}}{2}\)
Áp dụng định lý Pythagoras trong tam giác DMC vuông tại M, ta có:
\(MH^2+HC^2=MC^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{x^2-25}}{2}\right)^2+\left(\dfrac{x-5}{2}\right)^2=18\)
\(\Leftrightarrow\dfrac{x^2-25}{4}+\dfrac{x^2-10x+25}{4}=18\)
\(\Leftrightarrow2x^2-10x=72\)
\(\Leftrightarrow x^2-5x-36=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\left(nhận\right)\\x=-4\left(loại\right)\end{matrix}\right.\)
Vậy \(BC=9\)