Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tìm bội chung nhỏ nhất (3,4,6)=12
Ta có A/4=A/3=A/2 và A+B+C=180 độ
Xét......
Ta có:A/4=B/3=C/2=A/4+B/3+C/2=?
Ta có các số đo tam giác đó tỉ lệ nghịch với 3, 4, 6
\(\Rightarrow\frac{\widehat{A}}{\frac{1}{3}}=\widehat{\frac{B}{\frac{1}{4}}}=\widehat{\frac{C}{\frac{1}{6}}}\)
\(ADTCDTSBN:\widehat{\frac{A}{\frac{1}{3}}}=\widehat{\frac{B}{\frac{1}{4}}}=\widehat{\frac{C}{\frac{1}{6}}}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{\frac{1}{3}+\frac{1}{4}+\frac{1}{6}}=\frac{180^o}{\frac{3}{4}}=240\)
\(\Rightarrow\widehat{\frac{A}{\frac{1}{3}}}=240\Rightarrow\widehat{A}=80^o\)
\(\widehat{\frac{B}{\frac{1}{4}}}=240\Rightarrow\widehat{B}=60^o\)
\(\widehat{\frac{C}{\frac{1}{6}}}=240\Rightarrow\widehat{C}=40^o\)
Vậy \(\widehat{A}=80^o;\widehat{B}=60^o;\widehat{C}=40^o\)

gọi x,y,z là số đo các góc trong tam giác ABC tỉ lệ nghịch với 6; 10; 15.
theo đề cho ta có:
6x=10y=15z hay 6x30=10y30=15z30⇒x5=y3=z2
và x+y+z= 180
x5=y3=z2=x+y+z5+3+2=18010=18
x=18.5=90
y=18.3=54
z=18.2=36
vậy số đo các góc trong tam giác ABC lần lượt là 90;54;36

vì số đo góc A;B;C lần lượt tỉ lệ nghịch với 3;4;6 nên :
3A = 4B = 6C
=> 3A/12 = 4B/12 = 6C/12
=> A/4 = B/3 = C/2
=> A+B+C/2+3+4 = A/4 = B/3 = C/2
A+B+C = 180
=> 180/9 = A/4 = B/3 = C/2
=> 20 = A/4 = B/3 = C/2
=> A = 80; B = 60; C = 40

Tổng số đo các góc của hình tam giác luôn bằng 360 độ
Số đo của góc A là:360:(3+5+7)x3=72 độ
Số đo của góc B là:72:3x5=120 độ
Số đo của góc C là:360-120-72=168 độ

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
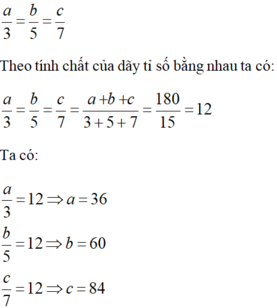
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o

Ta có: số đo 3 góc lần lượt là x;y;z
Ta có: \(\frac{15}{x}=\frac{16}{y}=\frac{18}{z}=\frac{15+16+18}{x+y+z}=\frac{49}{180}\)
Vậy số đo góc x là: \(x=\frac{15\times180}{49}=\frac{2700}{49}\)
Vậy số đo góc y là: \(y=\frac{16\times180}{49}=\frac{2880}{49}\)
Vậy số đo góc z là: \(z=\frac{18\times180}{49}=\frac{3240}{49}\)
Tam giác ABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (định lí tổng 3 góc của tam giác)
Theo đề bài : \(\frac{\widehat{A}}{\frac{1}{15}}=\frac{\widehat{B}}{\frac{1}{16}}=\frac{\widehat{C}}{\frac{1}{18}}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{\frac{1}{15}+\frac{1}{16}+\frac{1}{18}}=\frac{180^o}{\frac{133}{720}}\approx974\) (tính chất dãy tỉ số bằng nhau)
=> \(\widehat{A}\approx65^o\) ; \(\widehat{B}\approx61^o\) ; \(\widehat{C}\approx54^o\)
Bạn kiểm tra lại đề, thông thường số góc k lẻ vậy ![]()
Lời giải:
Tam giác $ABC$ vuông tại $C$ nên $\widehat{C}=90^0$.
$\widehat{A}+\widehat{B}=180^0-\widehat{C}=180^0-90^0=90^0$
Vì $\widehat{A}, \widehat{B}$ tỉ lệ nghịch với $\frac{1}{2}, \frac{2}{5}$ nên:
$\widehat{A}.\frac{1}{2}=\widehat{B}.\frac{2}{5}$
$\Rightarrow \widehat{A}=\widehat{B}.\frac{2}{5}:\frac{1}{2}=\widehat{B}.\frac{4}{5}$
$\Rightarrow \widehat{A}+\widehat{B}=\frac{9}{5}\widehat{B}$
$\Rightarrow 90^0=\frac{9}{5}\widehat{B}$
$\Rightarrow \widehat{B}=50^0$
$\widehat{A}=90^0-\widehat{B}=90^0-50^0=40^0$