
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





b: \(\sqrt{8-2\sqrt{15}}-\sqrt{5}\)
\(=\sqrt{5}-\sqrt{3}-\sqrt{5}\)
\(=-\sqrt{3}\)
c: \(\sqrt{11-6\sqrt{2}}=3-\sqrt{2}\)
d: \(\sqrt{5-2\sqrt{6}}=\sqrt{3}-\sqrt{2}\)

\(\Delta'=4-\left(m+1\right)\ge0\Rightarrow m\le3\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1^2+x_2^2=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=5\left(x_1+x_2\right)\)
\(\Leftrightarrow16-2\left(m+1\right)=20\)
\(\Leftrightarrow m=-3\) (thỏa mãn)
a. Ta có: \(x^2-4x+m+1=0\)
Thay m=2 ta được: \(x^2-4x+2+1=0\Leftrightarrow x^2-4x+3=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
b. Để phương trình có 2 nghiệm phân biệt thì \(\Delta=\left(-4\right)^2-4.1.\left(m+1\right)>0\)
\(\Leftrightarrow16-4\left(m+1\right)>0\Leftrightarrow16>4\left(m+1\right)\Leftrightarrow4>m+1\Leftrightarrow m< 3\)
Áp dụng định lí Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m+1\end{matrix}\right.\)
Theo đề ta có: \(x_1^2+x_2^2=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(4\right)^2-2\left(m+1\right)=5.4\)
\(\Leftrightarrow16-2m-2=20\Leftrightarrow m=-3\) (TM)

\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{3}y=\dfrac{7}{3}\\x-\dfrac{1}{2}y=-\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{6}y=\dfrac{5}{2}\\x+\dfrac{1}{3}y=\dfrac{7}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=\dfrac{4}{3}\end{matrix}\right.\)
Lời giải:
Lấy PT(1) trừ PT(2) theo vế:
$\frac{y}{3}+\frac{y}{2}=\frac{7}{3}+\frac{1}{6}$
$\Leftrightarrow \frac{5}{6}y=\frac{5}{2}$
$\Leftrightarrow y=3$
$x=\frac{7}{3}-\frac{y}{3}=\frac{7}{3}-1=\frac{4}{3}$

a) A = \(\sum\limits^{50}_1\left(2x\right)-\sum\limits^{50}_1\left(2x-1\right)\) = 5050
b) B = \(\sum\limits^{2010}_1x^3\) = 4084663313000




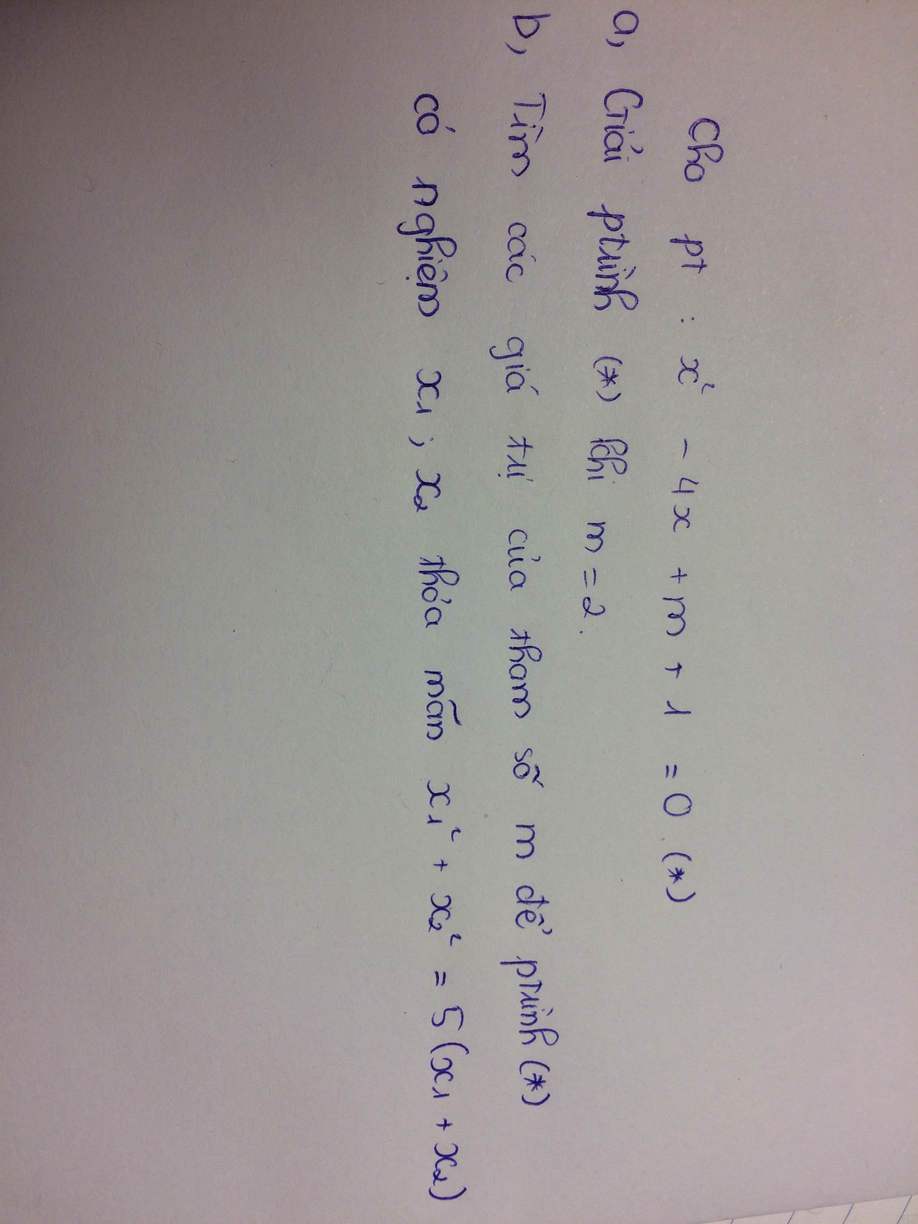


`tan (1/2) ≈ 26^o 33'`