Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^{202}-2000y^{2001}=2005\)
\(x^{202}=\left(x^{101}\right)^2\)là SCP nên chia 8 dư 0,1,4
\(2000y^{2001}⋮8\)=> VT chia 8 dư 0,1,4
Mà VP=2005 chia 8 dư 5
=> MT <=> Pt vô nghiệm
Mình làm hơn lằng nhằn nha:
Ta có:\(x^{202}=\left(x^{101}\right)^2\)là 1 số chính phương.Mà sô chính phương có dạng 4k+1 hoặc 4k\(\rightarrow\left(x^{101}\right)^2⋮4\)hoặc \(\div4\)dư 3
Mà \(2000y^{2001}⋮4\)
\(\Rightarrow\left(x^{101}\right)^2+2000y^{2001}⋮4\)hoặc \(\div4\)dư 3
Mà \(2005\div4\)dư \(1\)
\(\Rightarrow\)Phương trình vô nghiệm

4. \(\sqrt{x}+\sqrt{y}=6\sqrt{55}\)
\(6\sqrt{55}\) là số vô tỉ, suy ra vế trái phải là các căn thức đồng dạng chứa \(\sqrt{55}\)
Đặt \(\sqrt{x}=a\sqrt{55};\sqrt{y}=b\sqrt{55}\) với \(a,b\in N\)
\(\Rightarrow a+b=6\)
Xét các TH:
a = 0 => b = 6
a = 1 => b = 5
a = 2 => b = 4
a = 3 => b = 3
a = 4 => b = 2
a = 5 => b = 1
a = 6 => b = 0
Từ đó dễ dàng tìm đc x, y

Lời giải:
Từ $a+b> c\Rightarrow a+b-c>0$ (cái này hiển nhiên)
Từ $|a-b|< c\Leftrightarrow |a-b|^2< c^2$
$\Leftrightarrow (a-b)^2< c^2$
$\Leftrightarrow (a-b-c)(a-b+c)<0$
Với $c>0$ thì $a-b-c< a-b+c$ nên để tích âm thì $a-b-c<0< a-b+c$
Hay $a-b-c<0$ và $a-b+c>0$

* Giả sử cả 3 pt đều có nghiệm kép hoặc vô nghiệm ta có :
pt \(x^2-2ax+b=0\) (1) có \(\Delta_1'=\left(-a\right)^2-b=a^2-b\le0\)
pt \(x^2-2bx+c=0\) (2) có \(\Delta_2'=\left(-b\right)^2-c=b^2-c\le0\)
pt \(x^2-2cx+a=0\) (3) có \(\Delta_3'=\left(-c\right)^2-a=c^2-a\le0\)
\(\Rightarrow\)\(\Delta_1'+\Delta_2'+\Delta_3'=\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\le0\) (*)
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)>0\\b\left(3-b\right)>0\\c\left(3-c\right)>0\end{cases}\Leftrightarrow\hept{\begin{cases}3a>a^2\\3b>b^2\\3c>c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)< 3\left(a+b+c\right)-\left(a+b+c\right)=2\left(a+b+c\right)=6>0\)
trái với (*)
Vậy có ít nhất một phương trình có hai nghiệm phân biệt
cái kia chưa bt làm -_-


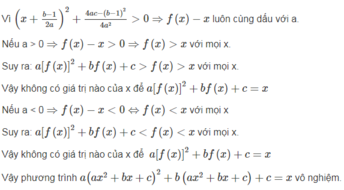
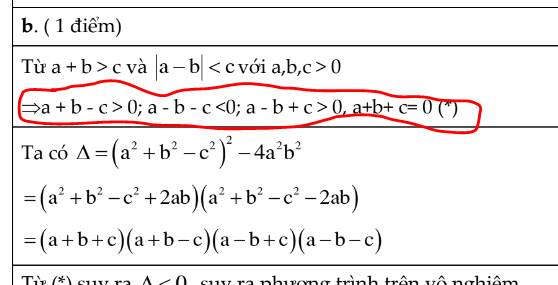
khó quá, không giải được
Em không chắc lắm
\(ĐKCĐ:a+b\ne0;a+c\ne0;b+c\ne0\)
\(\frac{x-ab}{a+b}+\frac{c-ac}{a+c}+\frac{x-bc}{b+c}=a+b+c\) (1)
\(\Leftrightarrow\left(\frac{x-ab}{a+b}-c\right)+\left(\frac{x-ac}{a+c}-b\right)+\left(\frac{x-bc}{b+c}-a\right)=0\)
\(\Leftrightarrow\frac{x-ab-ac-bc}{a+b}+\frac{x-ac-ab-bc}{a+c}+\frac{x-bc-ab-ac}{b+c}=0\)
\(\Leftrightarrow\left(x-ab-bc-ac\right)\left(\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}\right)=0\)
Phương trình (1) vô số nghiệm khi và chỉ khi \(\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}=0\) (2)
Ví dụ ta chọn a = 1 ; b = 1. Để (2) xảy ra ta chọn c sao cho:
\(\frac{1}{2}+\frac{1}{1+c}+\frac{1}{1+c}=0\Leftrightarrow\frac{2}{1+c}=\frac{1}{2}\Leftrightarrow c=-5\)
Vậy phương trình (1) vô số nghiệm chẳng hạn như a = 1; b = 1; c = -5
P/S: Em làm còn nhiều sai sót, mong các anh chị bỏ qua ạ