Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,=2x^2-10x+x^2+x-6=3x^2-9x-6\\ b,=x^2+4x+4-x^2+8x-15=12x-11\\ c,=4x^2-12x+9-4x^2+x=-11x+9\)

\(a,\dfrac{x^2+2}{x^3+1}-\dfrac{1}{x+1}\left(ĐKXĐ:x\ne-1\right)\\ =\dfrac{x^2+2-\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\\ c,\dfrac{1}{2-2x}-\dfrac{3}{2+2x}+\dfrac{2x}{x^2-1}\\ =\dfrac{-1}{2\left(x-1\right)}-\dfrac{3}{2\left(x+1\right)}+\dfrac{2x}{\left(x-1\right)\left(x+1\right)}\left(ĐKXĐ:x\ne\pm1\right)\\ =\dfrac{-1\left(x+1\right)-3\left(x-1\right)+2x.2}{2\left(x+1\right)\left(x-1\right)}\\ =\dfrac{-x-1-3x+3+4x}{2\left(x+1\right)\left(x-1\right)}=\dfrac{2}{2\left(x+1\right)\left(x-1\right)}=\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)

a: \(=15x^5-25x^4+15x^3\)
b: \(=2x^3+10x^2-8x-x^2-5x+4\)
\(=2x^3+9x^2-13x+4\)

a,\(\dfrac{3-x}{x-5}+\dfrac{2x-8}{x-5}=\dfrac{3-x+2x-8}{x-5}=\dfrac{x-5}{x-5}=1\)
b, \(\dfrac{1}{x-y}+\dfrac{1}{x+y}+\dfrac{2x}{x^2-y^2}=\dfrac{x+y}{\left(x-y\right)\left(x+y\right)}+\dfrac{x-y}{\left(x-y\right)\left(x+y\right)}+\dfrac{2x}{\left(x-y\right)\left(x+y\right)}=\dfrac{x+y+x-y+2x}{\left(x-y\right)\left(x+y\right)}=\dfrac{4x}{\left(x-y\right)\left(x+y\right)}\)

\(Bài1:\\ a,\left(4x-1\right)\left(2x^2-x-1\right)=4x\left(2x^2-x-1\right)-\left(2x^2-x-1\right)=8x^3-4x^2-4x-2x^2+x+1=8x^3-6x^2-3x+1\\ b,\left(4x^3+8x^2-2x\right):2x\\ =2x\left(2x^2+4x-1\right):2x\\ =2x^2+4x-1\)
\(Bài2:\\ a,2x^3-8x^2+8x=2x\left(x^2-4x+4\right)=2x\left(x-2\right)^2\\ b,2xy+2x+yz+z=2x\left(y+1\right)+z\left(y+1\right)=\left(y+1\right)\left(2x+z\right)\\ c,x^2+2x+1-y^2=\left(x+1\right)^2-y^2=\left(x-y+1\right)\left(x+y+1\right)\)

\(a,=4x^2-4x+1-4x^2+4-x^2-x+6=-x^2-5x+11\\ b,=8x^3+27-8x^3+72x=72x+27\)
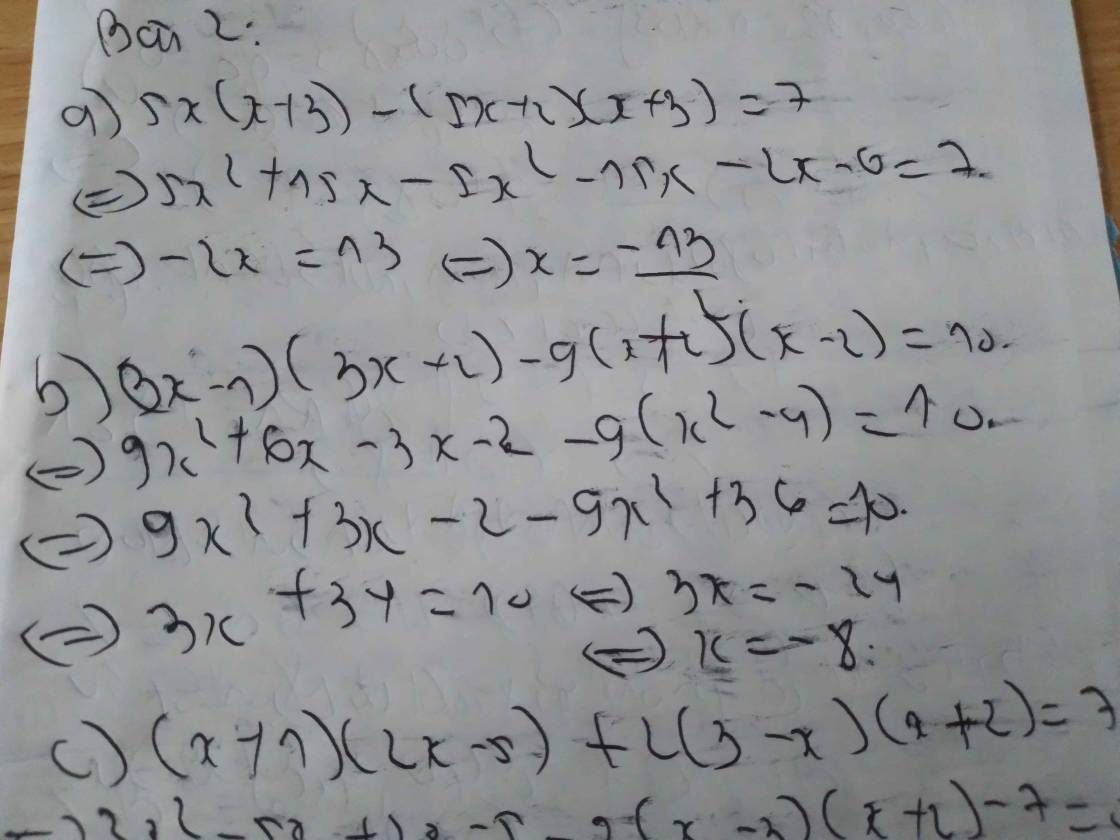


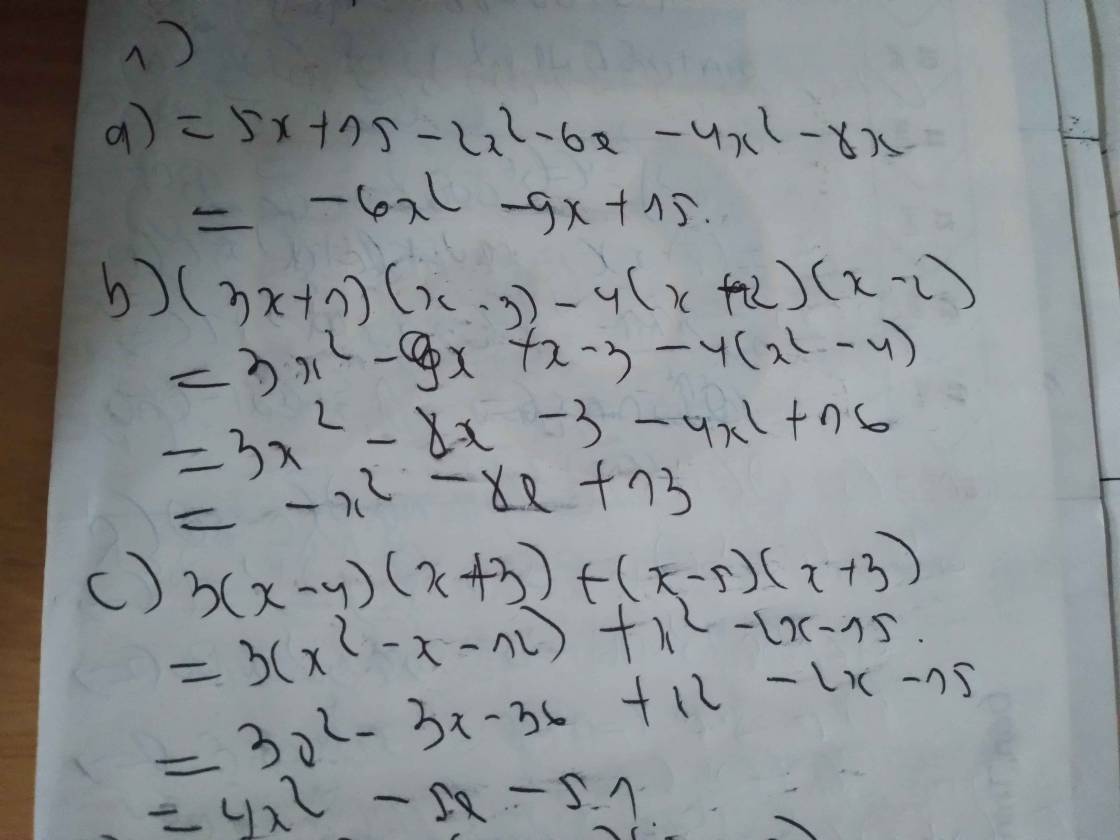
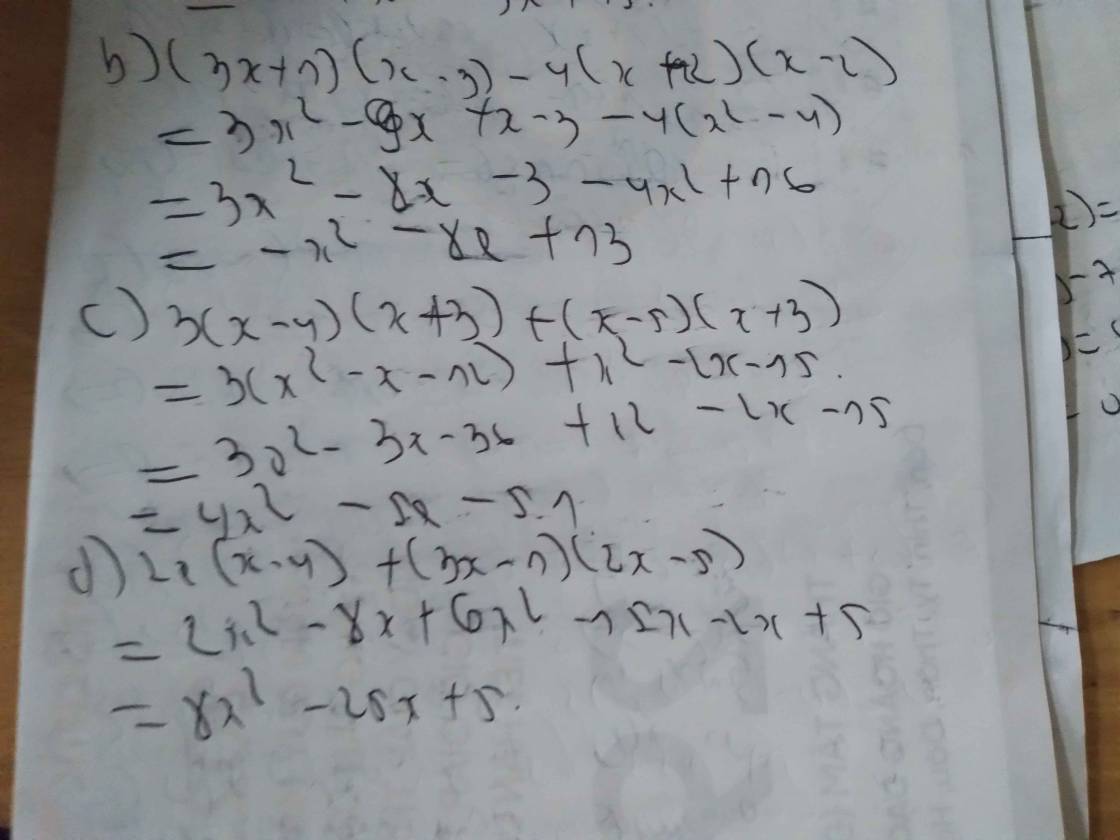
\(a.\) \((\frac{1}{2}x-1)(2x-3)\)
\(=\) \(x^2-\frac{3}{2}x-2x+3\)
\(=\) \(x^2-\frac{7}{2}x+3\)
\(b.\) \((x-7)(x-5)\)
\(=\) \(x^2-5x-7x+35\)
\(=\) \(x^2-12x+35\)
\(c.\) \((x-\frac{1}{2})(x+\frac{1}{2})(4x-1)\)
\(=\) \((x^2+\frac{1}{2}x-\frac{1}{2}x-\frac{1}{4})(4x-1)\)
\(=\) \((x^2-\frac{1}{4})(4x-1)\)
\(=\) \(4x^3-x^2-x+\frac{1}{4}\)
a, \(\left(\frac{1}{2}x-1\right)\left(2x-3\right)\)\(=x^2-\frac{3}{2}x-2x+3=x^2-\frac{7}{2}x+3\)
b, \(\left(x-7\right)\left(x-5\right)\)\(=x^2-5x-7x+35=x^2-12x+35\)
c, \(\left(x-\frac{1}{2}\right)\left(x+\frac{1}{2}\right)\left(4x-1\right)\)\(\left(x^2-\frac{1}{4}\right)\left(4x-1\right)=4x^3-x^2-x+\frac{1}{4}\)
Chúc học tốt!