Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có:
nm//ac
bm=cm
=>bn=na
=>nm là đtb của tam giác bac
=>nm = ca/2=0,4
vậy khoảng cánh chân của người đứng trên bật than đối với bức tường là 0,4 m

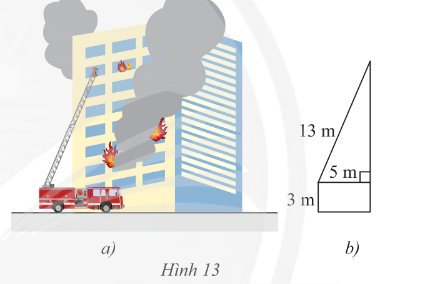
Gọi \(x\) là khoảng cách của xe đến đầu thang (m)
Áp dụng định lý Pythagore vào tam giác vuông trong hình ta có:
\({x^2} + {5^2} = {13^2}\)
\({x^2} = {13^2} - {5^2} = 144 = {12^2}\)
\(x = 12\) (m)
Chiều cao mà thang có thể vươn tới là:
\(12 + 3 = 15\) (m)

Khoảng cách từ điểm gỗ chạm vào tường trên mặt đất là:
\(\sqrt{2,6^2-1^2}=2,4\left(m\right)\)

a)
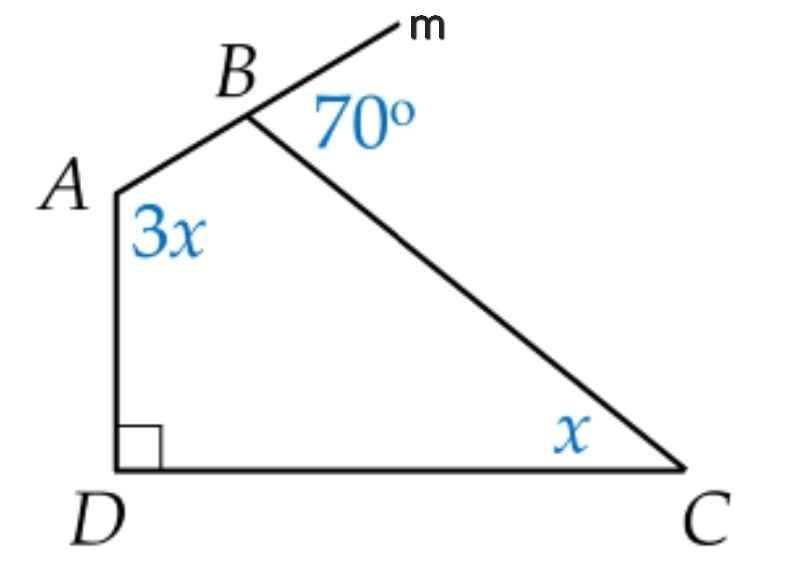 Ta có:
Ta có:
∠ABC + ∠CBm = 180⁰ (kề bù)
⇒ ∠ABC = 180⁰ - ∠CBm
= 180⁰ - 70⁰
= 110⁰
Tứ giác ABCD có:
∠A + ∠ABC + ∠C + ∠D = 360⁰ (tổng bốn góc trong tứ giác ABCD)
⇒ 3x + 110⁰ + x + 90⁰ = 360⁰
⇒ 4x + 200⁰ = 360⁰
⇒ 4x = 360⁰ - 200⁰
4x = 160⁰
⇒ x = 160⁰ : 4
⇒ x = 40⁰
b) ∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 3,7² - 1,2²
= 12,25
⇒ AH = 3,5
⇒ AH/BH = 3,5/1,2 ≈ 2,9 > 2,2
Vậy thang cách chân tường không "an toàn"

Do ${ABCD}$ là hình thang cân (gt) nên \(\widehat A = \widehat B\)
Xét hình thang \(ABCD\) ta có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} + \widehat {\rm{D}} = 360^\circ \)
\(\begin{array}{l}\widehat A + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat A + \widehat B = 210^\circ \end{array}\)
Mà \(\widehat A = \widehat B\) (cmt)
Suy ra : \(\widehat {\rm{A}} = \widehat B = 105^\circ \)


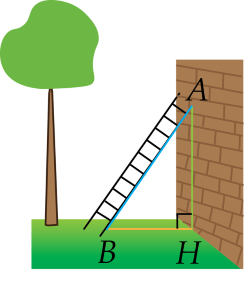

Gọi tam giác tạo thành là tam giác ABC
Với chiếc thang là cạnh huyền AC, khoảng cách của chân thang và chân tường là BC và chiều cao của bức tường là AB:
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2+AB^2}=\sqrt{1,5^2+6^2}\approx6,2\left(m\right)\)
Độ dài của chiếc thang nhỏ:
\(A'C'=\dfrac{2}{3}\cdot AC=\dfrac{2}{3}\cdot6,2\approx4,13\left(m\right)\)
Áp dụng định lý Py-ta-go ta tìm được độ cao mà thang đặt đến:
\(A'B'=\sqrt{A'C'^2-B'C'^2}=\sqrt{4,13^2-1^2}\approx4\left(m\right)\)
Điểm cao nhất của thang cách mặt bước tường là:
\(AB-A'B'=6-4=2\left(m\right)\)
Vậy....