
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Vì $a,b$ là số tự nhiên nên $2a+1,b-2$ là số nguyên
$(2a+1)(b-2)=12$ nên $2a+1$ là ước của $12$
Mà $2a+1$ là số tự nhiên lẻ nên $2a+1\in\left\{1;3\right\}$
Nếu $2a+1=1$ thì $b-2=12:1=12$
$\Rightarrow a=0; b=14$ (thỏa mãn)
Nếu $2a+1=3$ thì $b-2=12:3=4$
$\Rightarrow a=1; b=6$ (thỏa mãn)

=>2ab-3a+b-9=0
=>b(2a+1)-3a-4,5-*4,5=0
=>b(2a+1)-1,5(2a+1)=4,5
=>(2a+1)(b-1,5)=4,5
=>(2a+1)(2b-3)=9
=>\(\left(2a+1;2b-3\right)\in\left\{\left(1;9\right);\left(3;3\right);\left(9;1\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(0;6\right);\left(1;3\right);\left(4;2\right)\right\}\)

Bạn dùng phương pháp chặn `b` rồi tìm `a` nhé.
`8a^2 + 31b^2 = 2468 <=> 31b^2 <= 2468 <=> b^2 < 81 -> b = 1 -> 8.`
Từ đây tìm `a` theo `b` và nhớ thử lại nhé.

=>3b(4a-3)+20a-15=2820
=>(4a-3)(3b+5)=2820
=>a chia 4 dư 1, b chia 3 dư 2
Do đó: \(\left(a,b\right)\in\varnothing\)


vì a<b nhưng a.b=30
mà 30=6.5
=3.10
=1.30
=15.2
vậy a là các số: 5;3;1;2
và b là các số :6;10;30;15
tick cho mk nha bạn

vận dụng hằng đẳng thức thứ 3, ta có: (x+y).(x-y)=5
\(\Leftrightarrow\)x\(^2\)-y\(^2\)=5
\(\Leftrightarrow\)\(\hept{\begin{cases}x^2\\y^2=4\end{cases}=9}\)
\(\Leftrightarrow\) \(\hept{\begin{cases}x=3,-3\\y=2,-2\end{cases}}\)

\(A=3+3^2+3^3+...+3^{100}\)
\(3A=3^2+3^3+3^4+...+3^{101}\)
\(3A-A=\left(3^2+3^3+...+3^{101}\right)-\left(3+3^2+...+3^{100}\right)\)
\(2A=3^{101}-3\)
\(A=\left(3^{101}-3\right):2\)
Ta có : \(2A+3=3^{101}\)
\(→n=101\)
~ Ủng hộ nhé ~
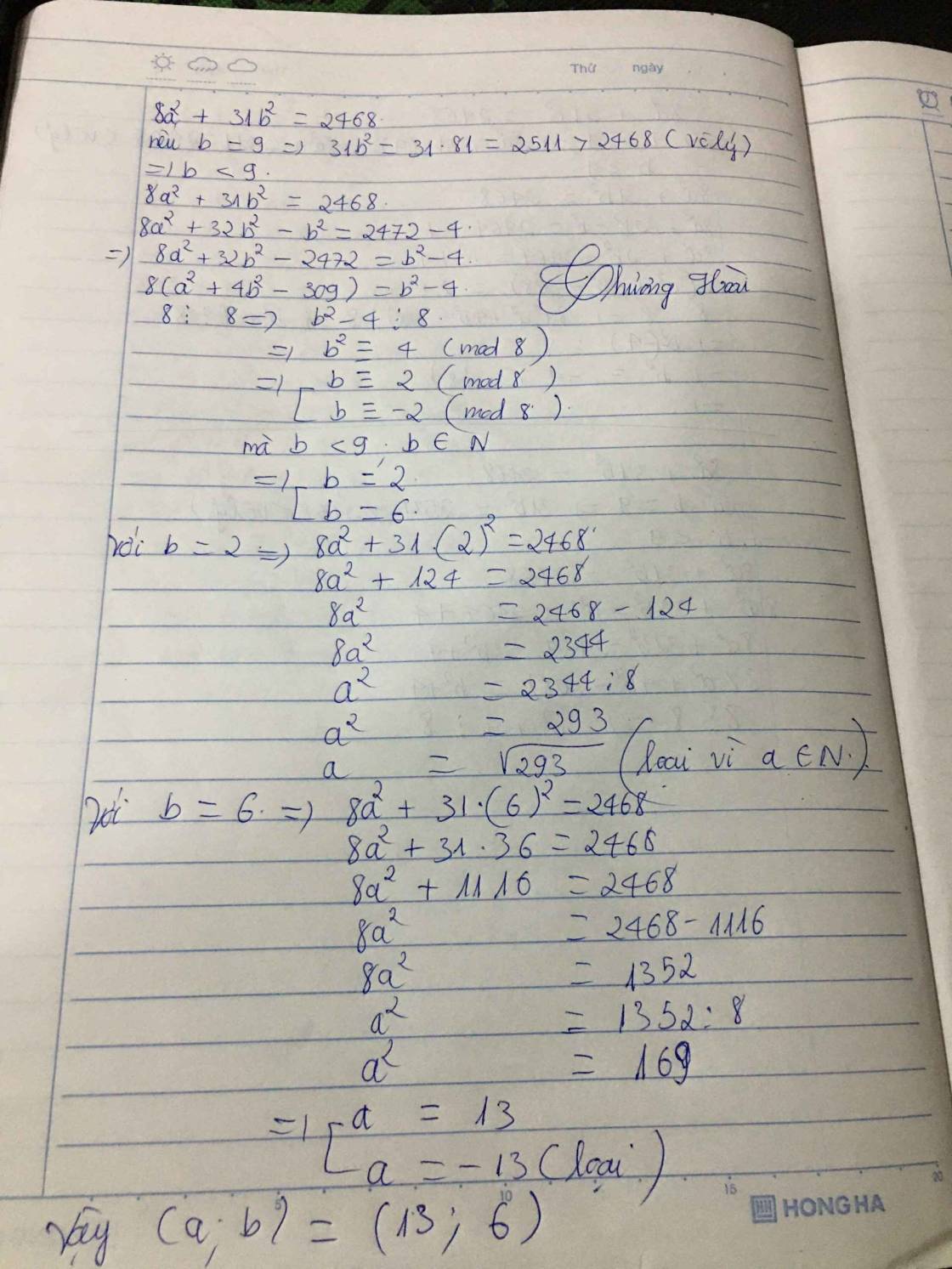
Ta có: 2a+a=3b
\(\Rightarrow\)a(2+1)=3b
\(\Rightarrow\)3a=3b
\(\Rightarrow\)a=b
2a + a = 3b
3a=3b
=>a/b=1
vậy a=b và a , b thuộc Z