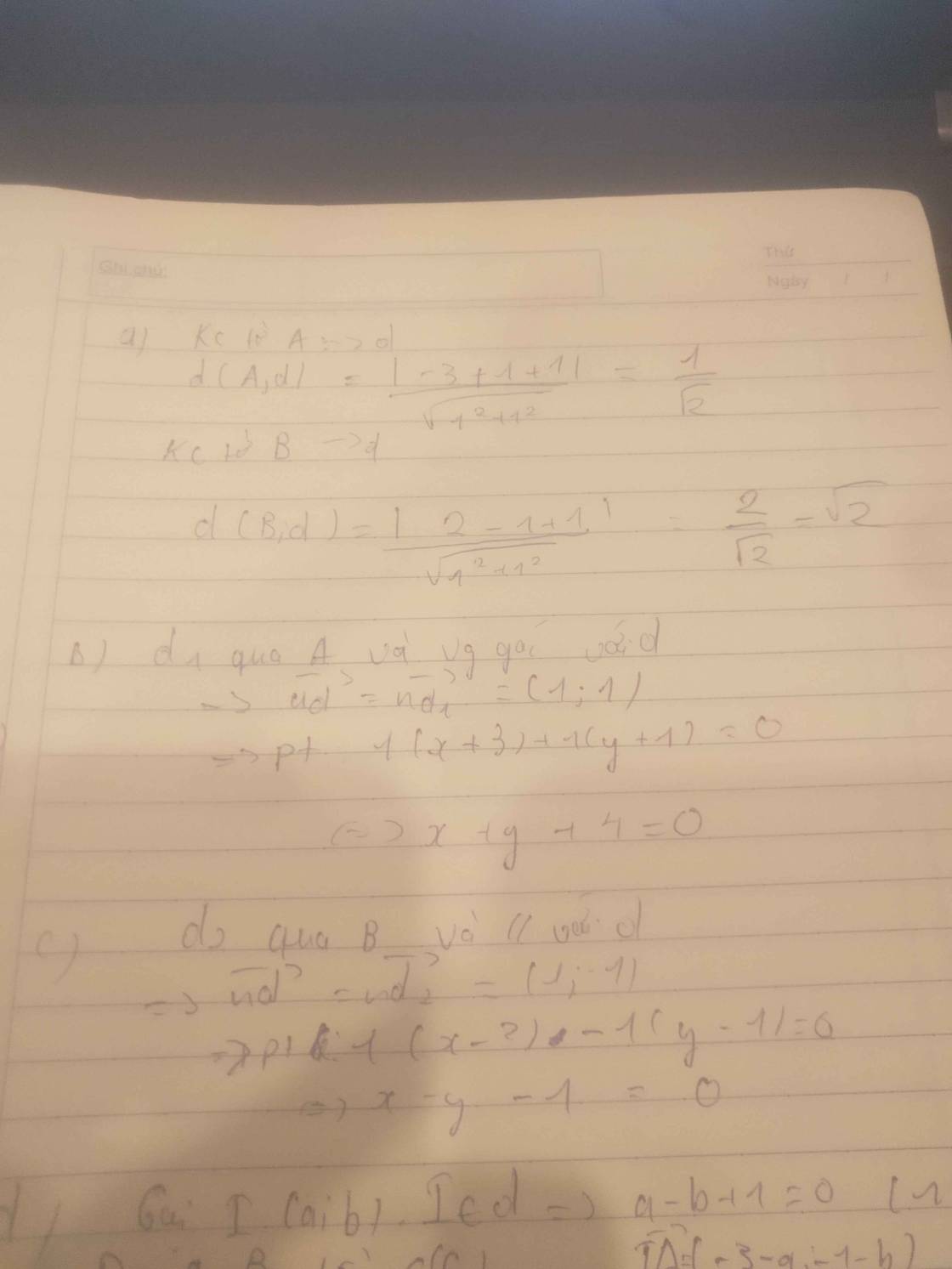a) Vì đồ thị hàm số ax+b song song với (d1) nên a=3

hay hàm số có dạng là y=3x+b

Vì đồ thị hàm số y=3x+b đi qua điểm C(3;-2)

nên Thay x=3 và y=-2 vào hàm số y=3x+b, ta được: 

\(3\cdot3+b=-2\)

\(\Leftrightarrow b+9=-2\)

hay b=-11

Vậy: Hàm số có dạng là y=3x-11

b) Vì (d)⊥(d2) nên \(a\cdot4=-1\)

hay \(a=-\dfrac{1}{4}\)

Vậy: Hàm số có dạng là \(y=-\dfrac{1}{4}x+b\)

Vì (d) đi qua D(2;-1) nên

Thay x=2 và y=-1 vào hàm số \(y=-\dfrac{1}{4}x+b\), ta được: 

\(-\dfrac{1}{4}\cdot2+b=-1\)

\(\Leftrightarrow b-\dfrac{1}{2}=-1\)

hay \(b=-\dfrac{1}{2}\)

Vậy: \(a=-\dfrac{1}{4}\) và \(b=-\dfrac{1}{2}\)

Thanks!❤️

1.

\(\left(C\right):x^2+y^2-2x-4=0\)

\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)

Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)

Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)

Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)

\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)

\(\Leftrightarrow m=-1\pm\sqrt{10}\)

\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)

2.

Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)

Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)

\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)

\(\Leftrightarrow m=-1\pm2\sqrt{2}\)

\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

1: Theo đề, ta có hệ phương trình:

\(\left\{{}\begin{matrix}3a+b=-2\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=1-2a=1-2\cdot\left(-3\right)=7\end{matrix}\right.\)

2: Vì (d)//y=-3x+2 nên a=-3

Vậy: y=-3x+b

Thay x=3 và y=3 vào y=-3x+b, ta được:

b-9=3

hay b=12

sao ngắn v bn @@

b, \(y=ax+b\left(d\right);y=x\left(d_1\right);y=-x+1\left(d_2\right);y=3x+5\left(d_3\right)\)

\(\left(d\right)//\left(d_1\right)\Rightarrow a=1\)

Phương trình hoành độ giao điểm của \(\left(d_2\right);\left(d_3\right)\) là

\(-x+1=3x+5\Leftrightarrow x=-1\Rightarrow y=2\Rightarrow\left(-1;2\right)\in\left(d_2\right);\left(d_3\right)\)

Do \(\left(d\right)\) đi qua giao điểm của \(\left(d_2\right);\left(d_3\right)\) nên \(\left(-1;2\right)\in\left(d\right)\)

\(\Rightarrow\left\{{}\begin{matrix}a=1\\-a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=3\end{matrix}\right.\)

Lời giải:
Vì $A\in (d_1)$ nên gọi tọa độ của $A$ là $(a, 2a-2)$

Vì $B\in (d_2)$ nên gọi tọa độ của $B$ là $(b, -b-3)$

$M$ là trung điểm của $AB$ nên:

\(3=x_M=\frac{x_A+x_B}{2}=\frac{a+b}{2}\Rightarrow a+b=6(1)\)

\(0=y_M=\frac{y_A+y_B}{2}=\frac{2a-2-b-3}{2}\Rightarrow 2a-b=5(2)\)

Từ $(1); (2)\Rightarrow a=\frac{11}{3}; b=\frac{7}{3}$

Khi đó: $A=(\frac{11}{3}, \frac{16}{3})$

Vì $A, M\in (d)$ nên VTCP của (d) là $\overrightarrow{MA}=(\frac{2}{3}, \frac{16}{3})$

$\Rightarrow \overrightarrow{n_d}=(\frac{-16}{3}, \frac{2}{3})$
PTĐT $(d)$ là:

$\frac{-16}{3}(x-3)+\frac{2}{3}(y-0)=0$
$\Leftrightarrow -8x+y+24=0$

tại sao lại ra 11/3 với 16/3 ạ

Gọi các đồ thị có CT chung là \(ax+b\)

\(a,\Leftrightarrow\left\{{}\begin{matrix}-a+b=-5\\a=0;b\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-5\end{matrix}\right.\Leftrightarrow\left(d_1\right):y=-5\\ b,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\a=2;b\ne-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=7\end{matrix}\right.\Leftrightarrow\left(d_2\right):y=2x+7\\ c,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\2a=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=3\end{matrix}\right.\Leftrightarrow\left(d_3\right):y=-2x+3\\ d,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-5\\b=0\end{matrix}\right.\Leftrightarrow\left(d_4\right):y=-5x\)

câu c bạn giải kỹ hơn đc ko 

(d) đi qua A, B => \(\overrightarrow{u_d}\) => \(\overrightarrow{n_d}\) => phương trình (d) biết vtpt và điểm đi qua

a. Gọi M là giao điểm của d1 và d2 => Tọa độ M là nghiệm của hệ:

\(\left\{{}\begin{matrix}2x+y-2=0\\x-y-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{5}{3}\\y=\frac{-4}{3}\end{matrix}\right.\) => M\(\left(\frac{5}{3};\frac{-4}{3}\right)\)

b. A ∈ d₁=> A(a; 2 - 2a) ; B ∈ d₂ => B (b ; b - 3)

Theo đề, ta có hệ: \(\left\{{}\begin{matrix}a+b=4\\-2a+b-1=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\frac{-5}{3}\\b=\frac{17}{3}\end{matrix}\right.\)

=> A(\(\frac{-5}{3};\frac{16}{3}\)) ; B(\(\frac{17}{3};\frac{8}{3}\))

=> (d): 4x + 11y - 52 = 0

  d lâu r ko làm ko nhớ -)(