Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Tập xác định: D = ℝ
Ta có ![]()
Xét m = 1, ta có y' = -3 < 0 ∀ x ∈ ℝ nên nghịch biến trên tập xác định.
Xét m ≠ 1 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi
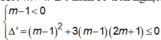
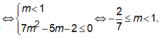
Vậy với - 2 7 ≤ m ≤ 1 thì hàm số y = ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5 nghịch biến trên tập xác định.

Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀ x ⇔ ∆ ' = 4m2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.

Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀x ⇔ Δ' = 4 m 2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.

Chọn B
Phương pháp:
Tính y'.
Tìm m để ![]()
Cách giải:
Ta có ![]()
![]()
Xét phương trình y' = 0 ![]() có
có ![]()
Suy ra phương trình y' = 0 luôn có hai nghiệm ![]()
Dễ thấy ![]() trong khoảng
trong khoảng ![]() thì hàm số đồng biến.
thì hàm số đồng biến.
Bài toán thỏa ![]()
Do ![]()
![]()
Vậy có ![]() giá trị của m thỏa mãn bài toán.
giá trị của m thỏa mãn bài toán.
Chú ý:
Cách khác: Tìm m để ![]()
Theo định lí Viet, ta có 
Hàm số đồng biến trên
(
2
;
+
∞
)
⇔
phương trình y' = 0 có hai nghiệm ![]()
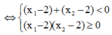
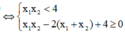

![]()
![]()
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)

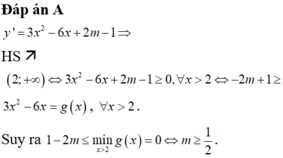


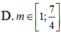

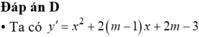
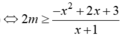
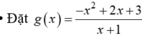
tại sao \(\frac{x1+x2}{2}< 2\) ạ
\(y'=g\left(x\right)=3x^2-2\left(m+1\right)x-\left(2m^2-3m+2\right)\)
Để hàm số đồng biến trên khoảng đã cho
\(\Leftrightarrow g\left(x\right)\ge0;\forall x\ge2\)
\(\Delta'=\left(m+1\right)^2+3\left(2m^2-3m+2\right)=7\left(m-\frac{1}{2}\right)^2+\frac{21}{4}>0;\forall m\)
\(\Rightarrow\) Để \(g\left(x\right)\ge0;\forall x\ge2\Leftrightarrow x_1< x_2\le2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-2\right)\left(x_2-2\right)\ge0\\\frac{x_1+x_2}{2}< 2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-2\left(x_1+x_2\right)+4\ge0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\frac{1}{3}\left(2m^2-3m+2\right)-\frac{4}{3}\left(m+1\right)+4\ge0\\\frac{2}{3}\left(m+1\right)< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2m^2-m+6\ge0\\2m< 10\end{matrix}\right.\) \(\Rightarrow-2\le m\le\frac{3}{2}\)