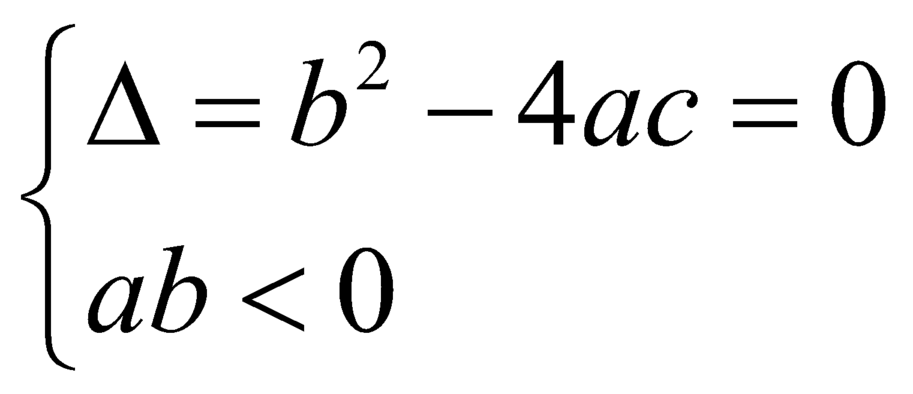Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
[Phương pháp tự luận]
Hàm số có cực đại , cực tiểu khi và chỉ khi m < 1
Tọa độ điểm cực trị A ( 0 ; m + 1 )
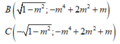
Phương trình đường thẳng BC: y + m 4 - 2 m 2 - m = 0
Vậy S đạt giá trị lớn nhất ⇔ m = 0
[Phương pháp trắc nghiệm]
Vậy S đạt giá trị lớn nhất ⇔ m = 0
Để hàm số có ba điểm cực trị khi và chỉ khi ab< 0 hay 1.( -2m) <0
Suy ra m> 0
Khi đó
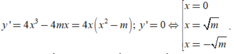
Suy ra tọa độ các điểm cực trị của đồ thị hàm số là:
A 0 ; 2 , B m ; - m 2 + 2 , C - m ; - m 2 + 2
Ycbt O A . O B . O C = 12 ⇔ 2 m + - m 2 + 2 2 = 12
Giải ra ta được m=2; có một giá trị nguyên.
Chọn B.
Đáp án C
Phương pháp:
+) Tính y’, giải phương trình y' = 0 ⇒ các cực trị của hàm số.
+) Tính các giá trị cực trị của hàm số và yCT.yCĐ < 0
Cách giải:
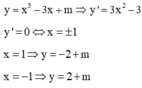
Giá trị cực đại và giá trị cực tiểu trái dấu ⇒ (-2 + m)(2 + m) < 0 ⇔ -2 < m < 2
Chọn C
Áp dụng công thức giải nhanh về khoảng cách
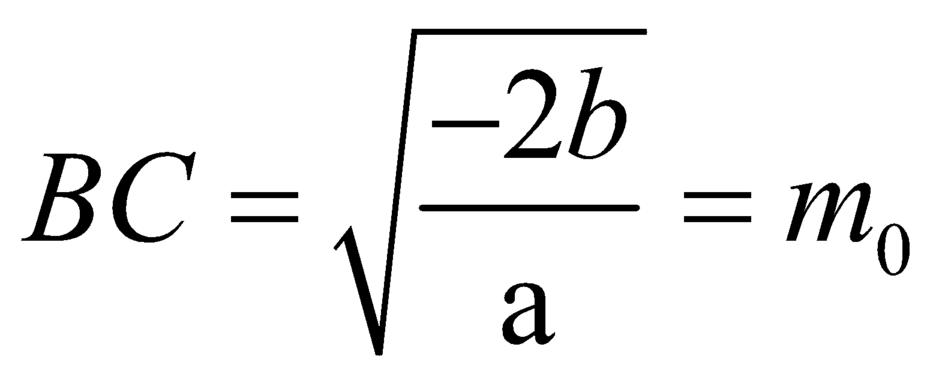của hai điểm cực tiểu (hoặc hai điểm cực đại): 
Chú ý: Các điểm cực trị đồ thị hàm số thuộc các trục tọa độ:
