a)\(234^{5^{6^7}}=234^{210}\)=...6

-Lũy thừa mà cơ số có tận cùng là 4, số mũ là số chẵn thì tận cùng của lũy thừa đó là 6

b) \(579^{6^{7^5}}=579^{210}\)=...1

-Lũy thừa mà cơ số có tận cùng là 4, số mũ là số chẵn thì tận cùng của lũy thừa đó là 1

sửa lại câu cuối cùng là 9 chứ ko phải 4 nhé

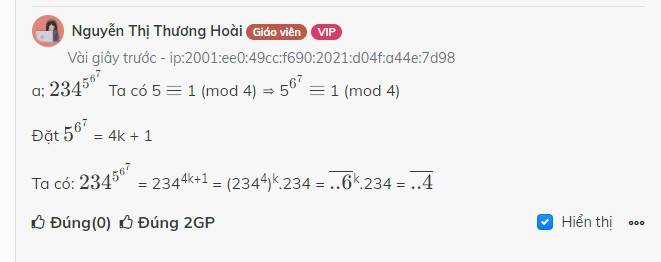
a; \(234^{5^{6^7}}\) Ta có 5 \(\equiv\) 1 (mod 4) ⇒ 5\(^{6^7}\) \(\equiv\) 1 (mod 4)

Đặt \(5^{6^7}\) = 4k + 1 

Ta có: \(234^{5^{6^7}}\) = 234^4k+1 = (234⁴)^k.234 = \(\overline{..6^{ }}\)^k.234 = \(\overline{..4}\) 

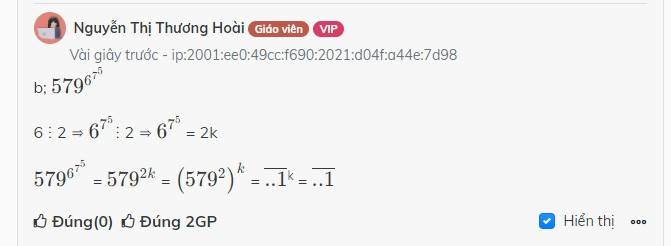
b; \(579^{6^{7^5}}\) 

6 ⋮ 2 ⇒ \(6^{7^5}\)⋮ 2 ⇒ \(6^{7^5}\) = 2k

\(579^{6^{7^5}}\) = \(579^{2k}\) = \(\left(579^2\right)^k\) = \(\overline{..1}\)^k = \(\overline{..1}\)

a)\(234^{5^{6^7}}=234^{210}\)=...6

-Lũy thừa mà cơ số có tận cùng là 4, số mũ là số chẵn thì tận cùng của lũy thừa đó là 6

b)\(579^{6^{7^5}}=579^{210}\)=...1

-Lũy thừa mà cơ số có tận cùng là 9, số mũ là số chẵn thì tận cùng của lũy thừa đó là 1

3629491209

chu so tan cung la 4 nha ban . Nho k cho minh nhe

Số 23 có tận cùng là 3.

Vì 210 = 208 + 2 nên 23 nâng lên luỹ thừa bậc 4n + 2.

Ta thấy x tận cùng là 3 mà nâng lên luỹ thừa bậc 4n + 2 thì tận cùng bằng 9 nên ((23⁵)⁶)⁷ tận cùng là 9.

7²⁰⁰⁶ = 7².(7⁴)⁵⁰¹ 

Vì (7⁴)⁵⁰¹  có chữ số tận cùng bằng 1

Nên 7²⁰⁰⁶  có chữ số tận cùng bằng 9 

3 không chia hết cho 2 nên 

\(3^{5^7}\) không chia hết cho 2 

Vậy A = 1999^2k+1

      A = (1999²)^k.1999

    A = \(\overline{...1}\)^k.1999

    A = \(\overline{..9}\)

Vì 6 ⋮ 2 nên \(6^{8^9}\) ⋮ 2

Vậy B = 2024^2k = (2024²)^k = \(\overline{..6}\)^k = \(\overline{..6}\)

           A = \(9999^{999^{99^9}}\)

Vì 999 không chia hết cho 2 nên \(999^{99^9}\) không chia hết cho 2 

Vậy \(999^{99^9}\) = 2k + 1

A = 9999^2k+1

A = (9999²)^k.9999

A = \(\overline{...1}\)^k. 9999

A = \(\overline{..1}\).9999

A = \(\overline{..9}\)

B = vì 8 ⋮ 2 nên \(8^{7^{6^{5^{3^2}}}}\) ⋮ 2

Vậy B = 9^2k = (9²)^k = \(\overline{..1}\)^k = \(\overline{..1}\)