Ta có:

M − 3 x y − 4 y 2 = x 2 − 7 x y + 8 y 2 ⇒ M = x 2 − 7 x y + 8 y 2 + 3 x y − 4 y 2 ⇒ M = x 2 + ( − 7 x y + 3 x y ) + 8 y 2 − 4 y 2 ⇒ A = 13 x 2 y + 3 y 3 − 10 x y 2

Chọn đáp án B

Chọn C

Ta có x2 + 2xy - 3x3 + 2y3 + 3x3-y3 = x2 + 2xy + y3.

Các nhóm đơn thức đồng dạng là:

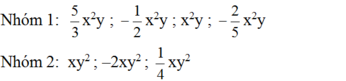
Vì nhóm 1 có phần biến chung là: x2y, nhóm 2 có phần biến chung là: xy2

Còn lại đơn thức xy (có phần biến là xy) không đồng dạng với các đơn thức nào đã cho.

\(\text{P= ax⁴y³ +10xy² +4y³ -2x⁴y³ -3xy²+bx³y⁴}\)

\(\text{P=}\text{ax⁴y³-2x⁴y³ +bx³y⁴ +10xy² -3xy² +4y³}\)

\(\text{P=}\text{(a-2)x⁴y³ + bx³y⁴ +(10-3)xy² +4y³}\)

\(\text{P=}\text{ (a-2)x⁴y³ + bx³y⁴ +7xy² +4y³}\)

\(\text{Để P có bậc 3 thì:}\)

\(a-2=0\Leftrightarrow a=2\)

\(b=0\Leftrightarrow b=0\)

\(\text{Vậy a=2,b=0 thì P có bậc là 3}\)

Gọi A = x2 + 2xy – 3x3 + 2y3 + 3x3 – y3

Trước hết ta thu gọn đa thức :

A = x2 + 2xy – 3x3 + 2y3 + 3x3 – y3

= (– 3x3+ 3x3) + x2 + 2xy + (2y3– y3)

= 0 + x2 + 2xy + y3.

= x2 + 2xy + y3.

Thay x = 5 ; y = 4 vào A ta được :

A = 52+ 2.5.4 + 43 = 25 + 40 + 64 = 129.

Vậy giá trị biểu thức x2 + 2xy – 3x3 + 2y3 + 3x3 – y3 tại x = 5 ; y = 4 bằng 129.

a) A = x² + 2xy – 3x³ + 2y³ + 3x³ – y³ tại x = 5 và y = 4.

Trước hết ta thu gọn đa thức

A = x² + 2xy – 3x³ + 2y³ + 3x³ – y³ = x² + 2xy + y³

Thay x = 5; y = 4 ta được:

A = 5² + 2.5.4 + 4³ = 25 + 40 + 64 = 129.

Vậy A = 129 tại x = 5 và y = 4.

b) M = xy - x²y² + x⁴y⁴ – x⁶y⁶ + x⁸y⁸ tại x = -1 và y = -1.

Thay x = -1; y = -1 vào biểu thức ta được:

M = (-1)(-1) - (-1)².(-1)² + (-1)^4. (-1)⁴-(-1)⁶.(-1)⁶ + (-1)⁸.(-1)⁸

= 1 -1 + 1 - 1+ 1 = 1.

a, x2 + 2xy - 3x3 + 2y3 + 3x3 - y3

= (-3x3 + 3x3)+(2y3 - y3)+ x2 + 2xy

= -1y3 + x2 + 2xy

thay x = 5 va y = 4 vao da thuc x2 + 2xy - 3x3 + 2y3 + 3x3 - y3

ta co:5.2 + 2.5.4 - 3.5.3 + 2.4.3 + 3.5.3 - 4.3

= 10 + 40 - 45 + 24 + 45 - 12

= 62

a) \(A+B=15x^2y-7xy^2-6y^3+2x^3-12x^2y+7xy^2=2x^3+3x^2y-6y^3\)

\(A-B=15x^2y-7xy^2-6y^3-2x^3+12x^2y-7xy^2=-2x^3-6y^3+27x^2y-14xy^2\)

     A+B = \(13x^2y-6y^3+2x^3\)

A-B = \(27x^2y-6y^3-2x^3\)

\(A+B=13x^2y-6y^3+2x^3\) tại x=1 ,y=3

\(A+B=13.1^2\)\(.3\) - \(6.3^3\)+\(2.1^3\)

A+B = 13.1.3 - 6.27 + 2.1

A+B = 39 - 162 + 2

A+B= -128

A-B = \(27.1^2.3-6.3^3-2.1^3\)

A-B = 27.1.3 - 6.27-2.1

A-B = 81 - 162 - 2 

A-B = -83

2,

M + N = 3xyz - 3x² + 5xy - 1 + 5x² + xyz - 5xy + 3 - y

= -3x² + 5x² + 3xyz + xyz + 5xy - 5xy - y - 1 + 3

= 2x² + 4xyz - y +2.

M - N = (3xyz - 3x² + 5xy - 1) - (5x² + xyz - 5xy + 3 - y)

= 3xyz - 3x² + 5xy - 1 - 5x² - xyz + 5xy - 3 + y

= -3x² - 5x² + 3xyz - xyz + 5xy + 5xy + y - 1 - 3

= -8x² + 2xyz + 10xy + y - 4.

N - M = (5x² + xyz - 5xy + 3 - y) - (3xyz - 3x² + 5xy - 1)

= 5x² + xyz - 5xy + 3 - y - 3xyz + 3x² - 5xy + 1

= 5x² + 3x² + xyz - 3xyz - 5xy - 5xy - y + 3 + 1

= 8x² - 2xyz - 10xy - y + 4.

3,

a) P + (x² – 2y²) = x² – y² + 3y² – 1

P = (x² – y² + 3y² – 1) - (x² – 2y²)

P = x² – y² + 3y² – 1 - x² + 2y²

P = x² – x² – y² + 3y² + 2y² – 1

P = 4y² – 1.

Vậy P = 4y² – 1.

b) Q – (5x² – xyz) = xy + 2x² – 3xyz + 5

Q = (xy + 2x² – 3xyz + 5) + (5x² – xyz)

Q = xy + 2x² – 3xyz + 5 + 5x² – xyz

Q = 7x² – 4xyz + xy + 5

Vậy Q = 7x² – 4xyz + xy + 5.

4,

a, Thu gọn : x2+2xy-3x3+2y3+3x3-y3

= x2+2xy+(-3x3+3x3)+2y3-y3

=x2+2xy+2y3-y3

Thay x=5,y=4 vào đa thức x2+2xy+2y3-y3 Ta có:

5² + 2.5.4 + 4³ = 25 + 40 + 64 = 129.

Vậy giá trị của đa thức x2+2xy+2y3-y3 tại x=5,y=4 là 129

b,

Thay x = -1; y = -1 vào biểu thức xy-x2y2+x4y4-x6y6+x8y8 Ta Có

M = (-1)(-1) - (-1)².(-1)² + (-1)^4. (-1)⁴-(-1)⁶.(-1)⁶ + (-1)⁸.(-1)⁸

= 1 -1 + 1 - 1+ 1 = 1.

Vậy giá trị của biểu thức xy-x2y2+x4y4-x6y6+x8y8 tại x=-1, y=-1 là 1

5,

a, C=A+B

C = x² – 2y + xy + 1 + x² + y - x²y² - 1

C = 2x² – y + xy - x²y²

b) C + A = B => C = B - A

C = (x² + y - x²y² - 1) - (x² – 2y + xy + 1)

C = x² + y - x²y² - 1 - x² + 2y - xy - 1

C = - x²y² - xy + 3y - 2.

dễ mà , có khó đâu bạn