Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2,
M + N = 3xyz - 3x2 + 5xy - 1 + 5x2 + xyz - 5xy + 3 - y
= -3x2 + 5x2 + 3xyz + xyz + 5xy - 5xy - y - 1 + 3
= 2x2 + 4xyz - y +2.
M - N = (3xyz - 3x2 + 5xy - 1) - (5x2 + xyz - 5xy + 3 - y)
= 3xyz - 3x2 + 5xy - 1 - 5x2 - xyz + 5xy - 3 + y
= -3x2 - 5x2 + 3xyz - xyz + 5xy + 5xy + y - 1 - 3
= -8x2 + 2xyz + 10xy + y - 4.
N - M = (5x2 + xyz - 5xy + 3 - y) - (3xyz - 3x2 + 5xy - 1)
= 5x2 + xyz - 5xy + 3 - y - 3xyz + 3x2 - 5xy + 1
= 5x2 + 3x2 + xyz - 3xyz - 5xy - 5xy - y + 3 + 1
= 8x2 - 2xyz - 10xy - y + 4.
3,
a) P + (x2 – 2y2) = x2 – y2 + 3y2 – 1
P = (x2 – y2 + 3y2 – 1) - (x2 – 2y2)
P = x2 – y2 + 3y2 – 1 - x2 + 2y2
P = x2 – x2 – y2 + 3y2 + 2y2 – 1
P = 4y2 – 1.
Vậy P = 4y2 – 1.
b) Q – (5x2 – xyz) = xy + 2x2 – 3xyz + 5
Q = (xy + 2x2 – 3xyz + 5) + (5x2 – xyz)
Q = xy + 2x2 – 3xyz + 5 + 5x2 – xyz
Q = 7x2 – 4xyz + xy + 5
Vậy Q = 7x2 – 4xyz + xy + 5.
4,
a, Thu gọn : x2+2xy-3x3+2y3+3x3-y3
= x2+2xy+(-3x3+3x3)+2y3-y3
=x2+2xy+2y3-y3
Thay x=5,y=4 vào đa thức x2+2xy+2y3-y3 Ta có:
52 + 2.5.4 + 43 = 25 + 40 + 64 = 129.
Vậy giá trị của đa thức x2+2xy+2y3-y3 tại x=5,y=4 là 129
b,
Thay x = -1; y = -1 vào biểu thức xy-x2y2+x4y4-x6y6+x8y8 Ta Có
M = (-1)(-1) - (-1)2.(-1)2 + (-1)4. (-1)4-(-1)6.(-1)6 + (-1)8.(-1)8
= 1 -1 + 1 - 1+ 1 = 1.
Vậy giá trị của biểu thức xy-x2y2+x4y4-x6y6+x8y8 tại x=-1, y=-1 là 1
5,
a, C=A+B
C = x2 – 2y + xy + 1 + x2 + y - x2y2 - 1
C = 2x2 – y + xy - x2y2
b) C + A = B => C = B - A
C = (x2 + y - x2y2 - 1) - (x2 – 2y + xy + 1)
C = x2 + y - x2y2 - 1 - x2 + 2y - xy - 1
C = - x2y2 - xy + 3y - 2.

Ta có
C − A − B = − x 2 + 3 x y + 2 y 2 − 4 x 2 − 5 x y + 3 y 2 − 3 x 2 + 2 x y + y 2 = − x 2 + 3 x y + 2 y 2 − 4 x 2 + 5 x y − 3 y 2 − 3 x 2 − 2 x y − y 2 = − x 2 − 4 x 2 − 3 x 2 + ( 3 x y + 5 x y − 2 x y ) + 2 y 2 − 3 y 2 − y 2 = − 8 x 2 + 6 x y − 2 y 2
Chọn đáp án B

Bài 2:
a: \(\left(x-8\right)\left(x^3+8\right)=0\)
=>\(\left[{}\begin{matrix}x-8=0\\x^3+8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8\\x^3=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
b: \(\left(4x-3\right)-\left(x+5\right)=3\left(10-x\right)\)
=>\(4x-3-x-5=30-3x\)
=>3x-8=30-3x
=>6x=38
=>\(x=\dfrac{38}{6}=\dfrac{19}{3}\)
Bài 6:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
b: Ta có: HB=HC
H nằm giữa B và C
Do đó: H là trung điểm của BC
=>\(HB=HC=\dfrac{8}{2}=4\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-4^2=9\)
=>\(AH=\sqrt{9}=3\left(cm\right)\)
c: Ta có: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H
d: Ta có: HD=HE
HE<HC(ΔHEC vuông tại E)
Do đó:HD<HC

`x^2-2y^2+2/3x^2y^3+B=2x^2+y^2+2/3x^2y^3`
`=>B=2x^2+y^2+2/3x^2y^3-x^2+2y^2-2/3x^2y^3`
`=>B=(2x^2-x^2)+(y^2+2y^2)+(2/3x^2y^3-2/3x^2y^3)`
`=>B=x^2+3y^2`
Thay `x=1 ; y=[-1]/3` vào `B` có:
`B=1^2+3.([-1]/3)^2=1+3 . 1/9=1+1/3=4/3`
`x^2 - 2y^2 + 2/3x^2y^3 + B = 2x^2 + y^2 + 2/3x^2y^3`
`=> B = 2x^2 + y^2 + 2/3x^2y^3` `- (x^2 - 2y^2 + 2/3x^2y^3)`
`= 2x^2 + y^2 + 2/3x^2y^3 - x^2 + 2y^2 - 2/3x^2y^3`
`= ( 2x^2 - x^2 ) + ( y^2 + 2y^2 ) + ( 2/3x^2y^3 - 2/3x^2y^3 )`
`= x^2 + 3y^2`
Thay `x=1 ; y=-1/3` vào `B` ta có `:`
`B = 1^2 + 3 . ( -1/3 )^2`
`= 1 + 1/3`
`= 4/3`

Có hai cách trình bày với bài này: một là bạn có thể liệt kê hết các phần tử ra hoặc bạn sắp xếp theo cùng thứ tự và tính như sau:

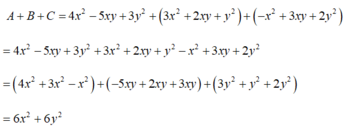
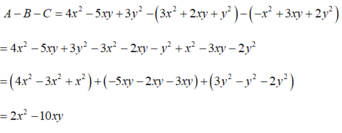
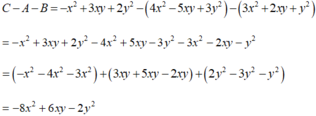
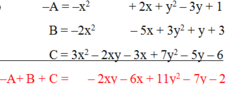
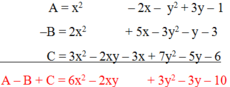
`Answer:`