Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D
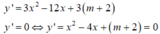
Hàm số có 2 điểm cực trị x1; x2 ⇔ Δ' > 0 ⇔ 4 - (m + 2) > 0 ⇔ m < 2
Chia y cho y’ ta được :
![]()
Suy ra : Phương trình đường thẳng đi qua hai điểm cực trị là: y = (m - 2)(2x + 1).
Điểm cực trị tương ứng : A(x1;(m - 2)(2x1 + 1)) và B(x2;(m - 2)(2x2 + 1))
Có:
![]()
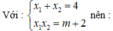
![]()


Chọn D
![]()
![]()
Hàm số có 2 điểm cực trị x 1 , x 2
![]()
Chia y cho y’ ta được :
![]()
Điểm cực trị tương ứng :
![]()
![]()
Với x 1 + x 2 = 4 x 1 x 2 = m + 2 nên y 1 y 2 = ( m - 2 ) 2 ( 4 m + 17 )
Hai cực trị cùng dấu ⇔ y 1 y 2 > 0
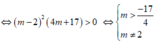
Kết hợp đk : - 17 4 < m < 2

Đáp án C
Phương pháp:
+) Tính y’, giải phương trình y' = 0 ⇒ các cực trị của hàm số.
+) Tính các giá trị cực trị của hàm số và yCT.yCĐ < 0
Cách giải:
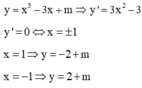
Giá trị cực đại và giá trị cực tiểu trái dấu ⇒ (-2 + m)(2 + m) < 0 ⇔ -2 < m < 2

\(\begin{cases}x^2+2\left|xy\right|-5x+m=0\left(1\right)\\x-y=\sin\left|x\right|-\sin\left|y\right|\left(2\right)\end{cases}\)
Biến đổi (2) về dạng : \(x-\sin\left|x\right|=y-\sin\left|y\right|\)
\(\Leftrightarrow f\left(x\right)=f\left(y\right)\) (*)
Xét hàm số \(f\left(t\right)=t-\sin\left|t\right|\)
- Miền xác định D=R
- Đạo hàm \(f'\left(t\right)=\begin{cases}1-\cot\left(t>0\right)\\1+\cot\left(t<0\right)\end{cases}\)
Suy ra \(f'\left(t\right)\ge0\) với mọi \(t\ne0\Leftrightarrow\) Hàm số đồng biến
Từ (*) \(\Leftrightarrow x=y\) Thay vào (1) ta có : \(3x^2-5x+m=0\) (**)
Để hệ có hai nghiệm với tung độ trái dấu \(\Leftrightarrow\) phương trình (**) có 2 nghiệm trái dấu \(\Leftrightarrow P<0\Leftrightarrow m<0\)
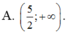
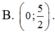
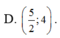
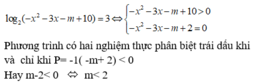


có hai cái nhé một cái ở câu hỏi và đề bài(dễ vc OK)
2 dấu + nha