Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ĐKXĐ: \(x\notin\left\{\dfrac{5}{2};-\dfrac{5}{2}\right\}\)

a) ∀ x , y ∈ ℝ
b) Chú ý: A 2 + B 2 ≥ 0 với ∀ A , B . Dấu "=" xảy ra khi A = 0 B = 0
Từ đó tìm được điều kiện xác định là: u ≠ 1 và v ≠ -2.

Bài 1:
a: ĐKXĐ: \(x+4\ne0\)
=>\(x\ne-4\)
b: ĐKXĐ: \(2x-1\ne0\)
=>\(2x\ne1\)
=>\(x\ne\dfrac{1}{2}\)
c: ĐKXĐ: \(x\left(y-3\right)\ne0\)
=>\(\left\{{}\begin{matrix}x\ne0\\y-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\y\ne3\end{matrix}\right.\)
d: ĐKXĐ: \(x^2-4y^2\ne0\)
=>\(\left(x-2y\right)\left(x+2y\right)\ne0\)
=>\(x\ne\pm2y\)
e: ĐKXĐ: \(\left(5-x\right)\left(y+2\right)\ne0\)
=>\(\left\{{}\begin{matrix}x\ne5\\y\ne-2\end{matrix}\right.\)
Bài 2:
a: \(\dfrac{-12x^3y^2}{-20x^2y^2}=\dfrac{12x^3y^2}{20x^2y^2}=\dfrac{12x^3y^2:4x^2y^2}{20x^2y^2:4x^2y^2}=\dfrac{3x}{5}\)
b: \(\dfrac{x^2+xy-x-y}{x^2-xy-x+y}\)
\(=\dfrac{\left(x^2+xy\right)-\left(x+y\right)}{\left(x^2-xy\right)-\left(x-y\right)}\)
\(=\dfrac{x\left(x+y\right)-\left(x+y\right)}{x\left(x-y\right)-\left(x-y\right)}=\dfrac{\left(x+y\right)\left(x-1\right)}{\left(x-y\right)\left(x-1\right)}\)
\(=\dfrac{x+y}{x-y}\)
c: \(\dfrac{7x^2-7xy}{y^2-x^2}\)
\(=\dfrac{7x\left(x-y\right)}{\left(y-x\right)\left(y+x\right)}\)
\(=\dfrac{-7x\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{-7x}{x+y}\)
d: \(\dfrac{7x^2+14x+7}{3x^2+3x}\)
\(=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\)
\(=\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
e: \(\dfrac{3y-2-3xy+2x}{1-3x-x^3+3x^2}\)
\(=\dfrac{3y-2-x\left(3y-2\right)}{1-3x+3x^2-x^3}\)
\(=\dfrac{\left(3y-2\right)\left(1-x\right)}{\left(1-x\right)^3}=\dfrac{3y-2}{\left(1-x\right)^2}\)
g: \(\dfrac{x^2+7x+12}{x^2+5x+6}\)
\(=\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x+3\right)\left(x+2\right)}\)
\(=\dfrac{x+4}{x+2}\)

a ĐKXĐ: x<>0; x<>3
b: Sửa đề; x^2-6x+9/x^2-3x
\(A=\dfrac{\left(x-3\right)^2}{x\left(x-3\right)}=\dfrac{x-3}{x}\)
c: Khi x=5 thì \(A=\dfrac{5-3}{5}=\dfrac{2}{5}\)

a, điều kiện xác định là \(x\ne1;x\ne-1\)
\(\frac{3x+3}{x^2-1}\)
\(=\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{3}{x-1}\)
b, để \(\frac{3x+3}{x^2-1}=-2\Rightarrow\frac{3}{x-1}=-2\)
\(\Rightarrow-2x+2=3\)
\(\Rightarrow-2x=1\)
\(\Rightarrow x=-\frac{1}{2}\)
a. ĐKXĐ: x2 - 1\(\ne\)0 (=) x \(\ne\)\(\pm\)1
b. \(\frac{3x+3}{x^2-1}\)
\(=\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{3}{x+1}\)với x \(\pm\)1
c. \(\frac{3}{x+1}=-2\)
\(\Rightarrow\)\(\left(x+1\right).\left(-2\right)=3\)
\(-2x-2=3\)
\(-2x=5\)
\(x=-\frac{5}{2}\)(t/m đk)

a) \(\dfrac{5x}{10}=\dfrac{x}{2}\)
b) \(\dfrac{4xy}{2y}=2x\left(y\ne0\right)\)
c) \(\dfrac{5x-5y}{3x-3y}=\dfrac{5}{3}\left(x\ne y\right)\)
d) \(\dfrac{x^2-y^2}{x+y}=x-y\left(đk:x\ne-y\right)\)
e) \(\dfrac{x^3-x^2+x-1}{x^2-1}=\dfrac{x^2+1}{x+1}\left(đk:x\ne\pm1\right)\)
f) \(\dfrac{x^2+4x+4}{2x+4}=\dfrac{x+2}{2}\left(đk:x\ne-2\right)\)
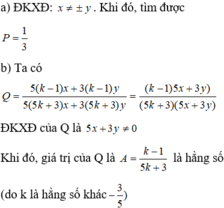

a) Xét mẫu của phân thức là \(x^2+2y^2+1\), ta có \(x^2\ge0;2y^2\ge0\Leftrightarrow x^2+2y^2\ge0\Leftrightarrow x^2+2y^2+1\ge1>0\)
Như vậy mẫu của phân thức không chỉ khác 0 mà thậm chí còn lớn hơn 0 nên ta không cần điều kiện của \(x,y\)
b) Điều kiện xác định \(\left(x-1\right)^2+\left(y+2\right)^2\ne0\)
Ta thấy \(\left(x-1\right)^2\ge0;\left(y+2\right)^2\ge0\)\(\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2\ge0\)
Nếu \(\left(x-1\right)^2+\left(y+2\right)^2=0\)thì \(\hept{\begin{cases}x-1=0\\y+2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-2\end{cases}}\)
Như vậy để phân thức đã cho xác định khi \(\hept{\begin{cases}x\ne1\\y\ne-2\end{cases}}\)