
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(x+a\right)\left(x^2+bx+16\right)\)
\(=x\left(x^2+bx+16\right)+a\left(x^2+bx+16\right)\)
\(=x^3+bx^2+16x+ax^2+abx+16a\)
\(=x^3+\left(a+b\right)x^2+\left(16+ab\right)x+16a\)
b) Ta có: \(\hept{\begin{cases}M=x^3+\left(a+b\right)x^2+\left(16+ab\right)x+16a\\N=x^3-64\end{cases}}\)
Cân bằng hệ số: \(\hept{\begin{cases}a+b=0\\16+ab=0\\16a=-64\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-4\\4\end{cases}}\)

Ta có: A = 4x – x 2 + 3
= 7 – x 2 + 4x – 4
= 7 – ( x 2 – 4x + 4)
= 7 – x - 2 2
Vì x - 2 2 ≥ 0 với mọi x nên A = 7 – x - 2 2 ≤ 7
Vậy giá trị của A lớn nhất là 7 khi x – 2 = 0 hay x = 2

a) Để \(\frac{17}{3-x}\) đạt giá trị nguyên lớn nhất
=> 3 - x đạt giá trị nhỏ nhất \(\left(3-x\ne0\right)\) ( x thuộc Z)
\(3-x\ge1\)
Dấu "=" xảy ra khi
3-x = 1
x = 2
=> giá trị lớn nhất của 17/3-x = 17/3-2 = 17/1 = 17
KL: giá trị lớn nhất của 17/3-x là 17 tại x = 2
b) Đặt \(B=\frac{32-2x}{11-x}=\frac{12+22-2x}{11-x}=\frac{12+2.\left(11-x\right)}{11-x}=\frac{12}{11-x}+2\)
Để B đạt giá trị nguyên lớn nhất
=> 12/11-x đạt giá trị nguyên lớn nhất
=> 11 - x đạt giá trị nguyên nhỏ nhất ( 11 - x khác 0, x thuộc Z)
\(11-x\ge1\)
Dấu "=" xảy ra khi
11 - x = 1
x = 10
=> giá trị lớn nhất của B là: B = 12/11-x +2 = 12/11-10 + 2 = 12/1 + 2 = 12 + 2 = 14
KL: giá trị lớn nhất của B = 14 tại x = 10

Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

Lời giải:
a. Áp dụng BĐT Cô-si:
$x^4+9\geq 6x^2$
$y^4+9\geq 6y^2$
$\Rightarrow x^4+y^4+18\geq 6(x^2+y^2)$
$A+18\geq 36$
$A\geq 18$
Vậy GTNN của $A$ là $18$ khi $x^2=y^2=3$
b.
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 2(x^2+y^2)\geq (x+y)^2$
$\Leftrightarrow 12\geq (x+y)^2$
$\Rightarrow B=x+y\leq \sqrt{12}$. Vậy $B$ max bằng $\sqrt{12}$ khi $x=y=\sqrt{3}$
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 6\geq 2C$
$\Leftrightarrow C\leq 3$. Vậy $C_{\max}=3$. Giá trị này đạt tại $x=y=-\sqrt{3}$

A+1 = x^2+6x+9/x^2+1 = (x+3)^2/x^2+1 >= 0
=> A >= -1
Dấu "=" xảy ra <=> x+3=0 <=> x=-3
Vậy GTNN của A = -1 <=> x=-3
Tk mk nha
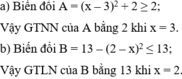
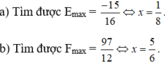

Ta có: A = -3 - x2 - x = -(x2 + x + 1/4) - 11/4 = -(x + 1/2)2 - 11/4
Ta luôn có: -(x + 1/2)2 \(\le\)0 \(\forall\)x
=> -(x + 1/2)2 - 11/4 \(\le\)-11/4 \(\forall\)x
Dấu "=" xảy ra khi: x + 1/2 = 0 <=> x = -1/2
Vậy Max của A = -11/4 tại x = -1/2
\(A=-3-x^2-x=-\left(x^2+x+3\right)=-\left[\left(x+\frac{1}{2}\right)^2+\frac{11}{4}\right]\)
Lại có : \(\left(x+\frac{1}{2}\right)^2\ge0=>A\le\frac{11}{4}\)
Dấu "=" xảy ra khi \(x+\frac{1}{2}=0=>x=-\frac{1}{2}\)
Vậy \(A_{max}=\frac{11}{4}\)khi \(x=-\frac{1}{2}\)