Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P = \(\left[x+2sprt\left(x\right)+5\right]\backslash\left[sprt\left(x\right)+1\right] \) là sao bn


\(x+y=1\Rightarrow x=1-y\)
\(C=x^2+y^2+xy=\left(1-y\right)^2+y^2+\left(1-y\right)y\)
\(=y^2-y+1\)\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)
=>minC=\(\dfrac{3}{4}\) \(\Leftrightarrow y=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{2}\)
Ta có :
\(x+y=1\Rightarrow\left(x+y\right)^2=1\)
\(\Leftrightarrow x^2+2xy+y^2=1\)
\(\Leftrightarrow x^2+xy+y^2=1-xy\ge1-\left(\dfrac{x+y}{2}\right)^2=1-\dfrac{1}{4}=\dfrac{3}{4}\)
Hay \(C \ge \dfrac{3}{4}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

ĐK: \(x\ge0\)
+) Với x = 0 => A = 0
+) Với x khác 0
Ta có: \(\frac{1}{A}=\frac{3}{4}\sqrt{x}-\frac{3}{4}+\frac{3}{4\sqrt{x}}=\frac{3}{4}\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)-\frac{3}{4}\ge\frac{3}{4}.2-\frac{3}{4}=\frac{3}{4}\)
=> \(A\le\frac{4}{3}\)
Dấu "=" xảy ra <=> \(\sqrt{x}=\frac{1}{\sqrt{x}}\)<=> x = 1
Vậy max A = 4/3 tại x = 1
Còn có 1 cách em quy đồng hai vế giải đenta theo A thì sẽ tìm đc cả GTNN và GTLN


\(A=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)=\left(x^2+5x-6\right)\left(x^2+5x+6\right)=\left(x^2+5x\right)^2-36\ge-36\)
\(minA=-56\Leftrightarrow x^2+5x=0\Leftrightarrow x\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(B=4x-x^2+1=-\left(x^2-4x+4\right)+5=-\left(x-2\right)^2+5\le5\)
\(maxB=5\Leftrightarrow x=2\)
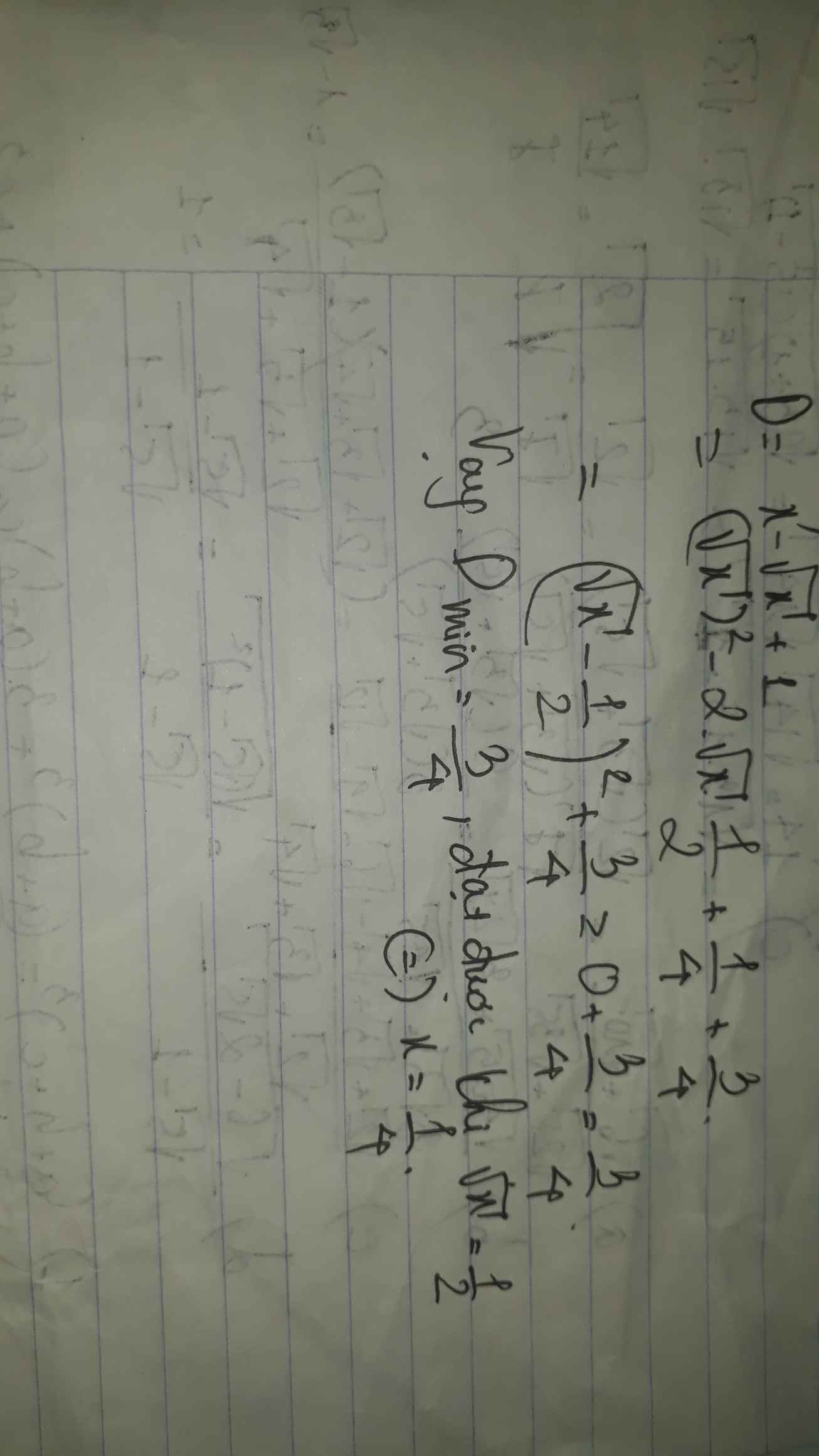
ĐKXĐ: x>=-1
\(A=x-2\sqrt{x+1}+30\)
\(=x+1-2\sqrt{x+1}+1+28\)
\(=\left(\sqrt{x+1}-1\right)^2+28>=28\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x+1}-1=0\)
=>\(\sqrt{x+1}=1\)
=>x+1=1
=>x=0