Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hoành độ giao điểm là nghiệm của PT:
x − 4 = − 2 x + 5 x − 2 ⇔ x 2 − 6 x + 8 = − 2 x + 5 x ≠ 2
⇔ x 2 − 4 x − 13 = 0 . Vậy trung điểm I của MN có hoành độ x = 2 ⇒ y = − 2 .

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

Đáp án B
Để ý thấy lời giải bài toán sai ở bước 3 do m có thể nhỏ hơn 0

Đáp án C
Ta có: y’ = 3x2 + 2(m+1)x – (3m+2)
Hàm số đồng biến trên khoảng (0;1)
3x2 + 2(m+1)x – (3m+2) ≥ 0 ∀ x ∈ (0;1)
⇔ m ≤ − 3 x 2 + 2 x − 2 2 x − 3 ∀ x ∈ (0;1)
Xét hàm số: g = − 3 x 2 + 2 x − 2 2 x − 3 D =(0;1)
Ta có: g’ = − 6 x 2 − 18 x − 2 ( 2 x − 3 ) 2
ð g’ = 0 ⇔ x = 9 ± 93 6 (không thoản mãn)
Ta có bảng biến thiên
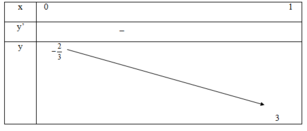
Vậy với m ≤ 3 hàm số đồng biến trên khoảng (0;1)

Chọn B.
Phương pháp:
Giải phương trình hoành độ giao điểm của hai đồ thị hàm số. Tìm tọa độ giao điểm M và N. Tìm tọa độ trung điểm I của MN.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hai hàm số
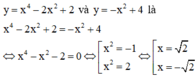
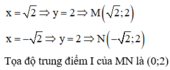

Xét hàm số y = f x = x - 2 + 4 - x trên đoạn 2 , 4 có:

Ta có:
![]()
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = x - 2 + 4 - x lần lượt là M = 2 ; m = 2
Chọn: D

Chọn C.
Tập xác định của hàm số ![]()
Cách 1: Bấm máy tính. Với máy 580vn chọn start:-2, end: 2, step: 2/9 có: ![]()
thử thấy phương án C gần nhất với kết quả này nên ta chọn C.
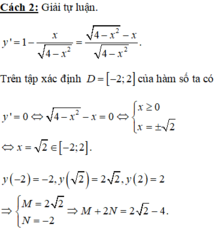


Đáp án là D.
• Ta có: y , = - 1 - 1 ( 2 + x ) 2 cho y , = 0 ⇔ x = - 1 x = - 3
• Bảng biến thiên:
Từ BBT ta có: m i n - 4 ; - 2 y = 7