
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với mọi x ta có :
\(\left|x+5\right|\ge0\)
\(\Leftrightarrow\left|x+5\right|+5\ge0\)
\(\Leftrightarrow A\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy..

Ta có | x + 1 | \(\ge\)0 \(\forall\)x
=> 5 . | x + 1 | \(\ge\)0 \(\forall\)x
=> 2018 + 5 . | x + 1 | \(\ge\)2018 \(\forall\)x
Dấu " = " xảy ra <=> x + 1 = 0 => x = -1
Vậy, GTNN của A = 2018 khi và chỉ khi x = -1
ta có :|x+1| >=0
=> 5|x+1|>=0
=> 2018+5|x+1|>= 2018
dấu = xảy ra khi |x+1|=0
x+1=0
x=-1
vay gtnn cua bieu thuc tren la 2018 khi x=-1

Bài giải
Nếu đề là \(F=\frac{1}{\left|x\right|}+2017\) thì làm như sau :
* Tìm giá trị lớn nhất :
\(\Rightarrow\text{ Vì }\frac{1}{\left|x\right|}>0\text{ và F lớn nhất }\Rightarrow\text{ }\frac{1}{\left|x\right|}\text{ lớn nhất }\)
\(\Leftrightarrow\text{ }\left|x\right|\text{ bé nhất }\left(x\ne0\right)\)
\(\Rightarrow\text{ }\left|x\right|\text{ là số nguyên dương nhỏ nhất }\Rightarrow\text{ }\left|x\right|=1\text{ }\Rightarrow\orbr{\begin{cases}x=-1\\x=1\end{cases}}\)
\(\Rightarrow\text{ }F=\frac{1}{\left|x\right|}+2017< 1+2017=2018\)
\(\text{Vậy }Max\text{ }F=2018\)
* Gía trị bé nhất không tìm được nha !
Bài giải
Làm nốt trường hợp còn lại bạn Rain nói nha ! Vì đề bạn ghi không rõ mới làm thế này nha ! TH2 : \(F=\frac{1}{\left|x\right|+2017}\)
* Gía trị lớn nhất
\(F=\frac{1}{\left|x\right|+2017}\text{ đạt giá trị lớn nhất khi }\left|x\right|+2017\text{ đạt GTNN }\)
Mà \(\left|x\right|\ge0\text{ }\Rightarrow\text{ }\left|x\right|+2017\ge2017\)
\(\text{ Vậy để }F\text{ lớn nhất thì }\left|x\right|+2017=2017\text{ Dấu " = " xảy ra khi }\left|x\right|=0\text{ }\Rightarrow\text{ }x=0\)
\(\text{Vậy }Max\text{ }F=\frac{1}{2017}\)
* Gía trị nhỏ nhất cũng không tìm được nha bạn !

A= |x+1|+5
Vì |x+1| > hoặc =0 => |x+1|+5 > hoặc =5
Dấu = xảy ra <=> x+1=0=> x=-1
Vậy A đạt GTNN =5 <=> x=-1
Còn câu b bạn tự làm
ủng hộ nha

|x+1|> hoặc = 0 với mọi x
suy ra |x+1|+5 > hoặc = 5 với mọi x
suy ra Amin=5 khi |x+1|=0
suy ra x+1=0
suy ra x = -1
vậy gtnn của A là 5 khi x=-1
bn nên sử dụng dấu suy ra và dấu lớn hơn hoặc vì mình ko biết đánh dấu . câu b bn làm tương tự vì x^2 cũng lớn hơn hoặc bằng 0

a) Ta có : A = - 15 - |7 - x| = -(15 + |7 - x|)
vì \(\left|7-x\right|\ge0\forall x\Rightarrow15+\left|7-x\right|\ge15\Rightarrow-\left(15+\left|7-x\right|\right)\le-15\)
Dấu"=" xảy ra <=> 7 - x = 0
=> x = 7
Vậy GTLN của A là - 15 khi x = 7
b) Ta có : \(\hept{\begin{cases}\left|x+2,5\right|\ge0\forall x\\\left(y-1\right)^4\ge0\forall y\end{cases}\Rightarrow\left|x+2,5\right|+\left(y-1\right)^4\ge0}\)
=> \(\left|x+2,5\right|+\left(y-1\right)^4-6\ge-6\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+2,5=0\\y-1=0\end{cases}\Rightarrow\hept{\begin{cases}x=-2,5\\y=1\end{cases}}}\)
Vậy GTNN của B là - 6 khi \(\hept{\begin{cases}x=-2,5\\y=1\end{cases}}\)
a) Vì \(\left|7-x\right|\ge0\forall x\)\(\Rightarrow-15-\left|7-x\right|\le-15\forall x\)
hay \(A\le-15\)
Dấu " = " xảy ra \(\Leftrightarrow7-x=0\)\(\Leftrightarrow x=7\)
Vậy \(maxA=-15\Leftrightarrow x=7\)
b) Vì \(\hept{\begin{cases}\left|x+2,5\right|\ge0\forall x\\\left(y-1\right)^4\ge0\forall y\end{cases}}\)\(\Rightarrow\left|x+2,5\right|+\left(y-1\right)^4\ge0\forall x,y\)
\(\Rightarrow\left|x+2,5\right|+\left|y-1\right|^4-6\ge-6\forall x,y\)
hay \(B\ge-6\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}x+2,5=0\\y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-2,5\\y=1\end{cases}}\)
Vậy \(minB=-6\Leftrightarrow\hept{\begin{cases}x=-2,5\\y=1\end{cases}}\)

a, \(A=\left|x-2017\right|+\left|2018-x\right|\ge\left|x-2017+2018-x\right|=1\)
Vậy \(Min=1\Leftrightarrow2017\le x\le2018\)
b, \(B=\dfrac{x^2+4+8}{x^2+4}=1+\dfrac{8}{x^2+4}\)
Thấy : \(x^2+4\ge4\)
\(\Rightarrow B=1+\dfrac{8}{x^2+4}\le3\)
Vậy \(Max=3\Leftrightarrow x=0\)
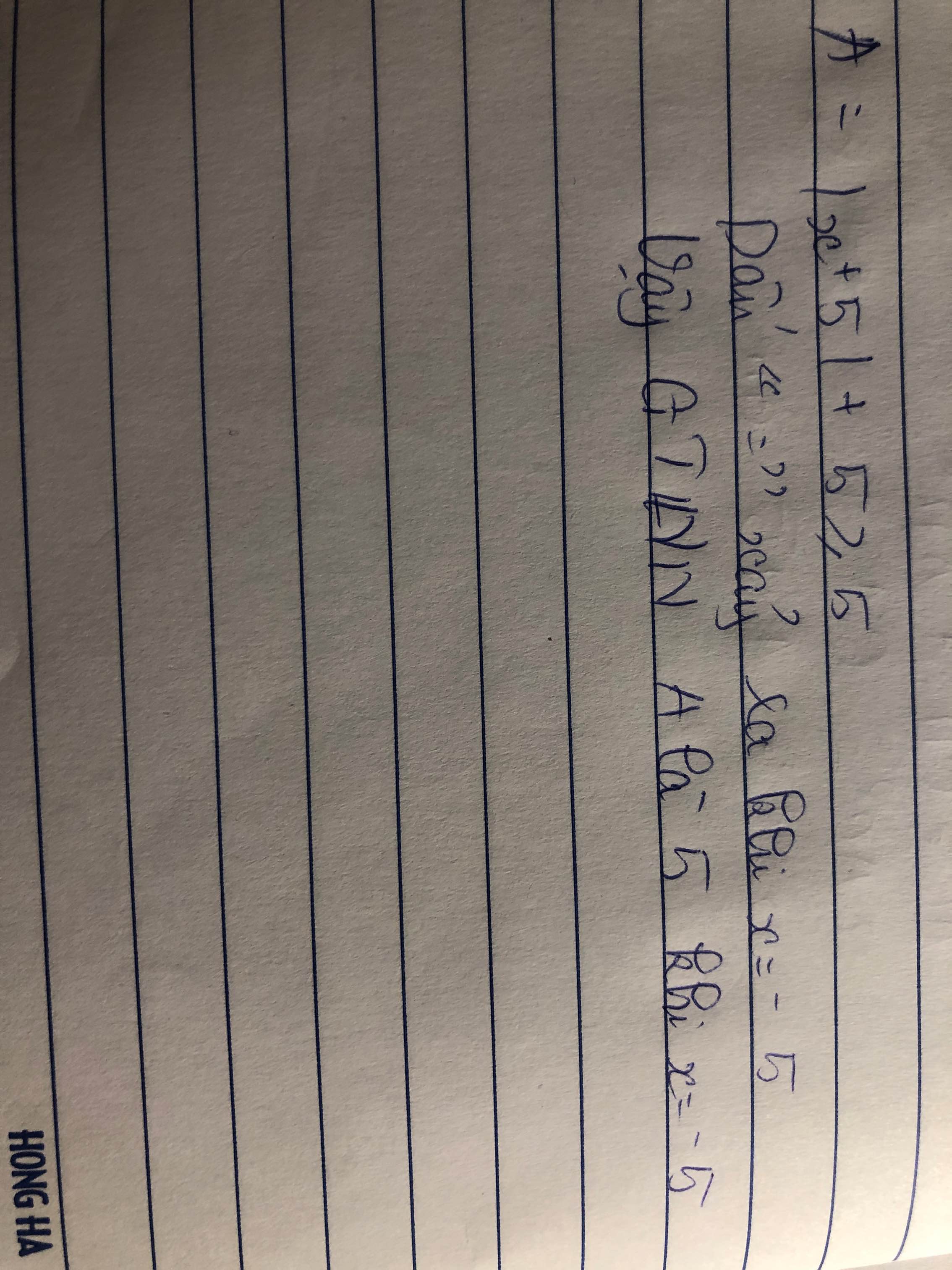
\(A=\left(x-4\right)^2+1\)
Ta có: \(\left(x-4\right)^2\ge0\Rightarrow\left(x-4\right)^2+1\ge1\Rightarrow A\ge1\)
\(A_{min}=1\Leftrightarrow x=4\)
\(B=\left|3x-2\right|-5\)
Ta có: \(\left|3x-2\right|\ge0\Rightarrow\left|3x-2\right|-5\ge-5\Rightarrow B\ge-5\)
\(B_{min}=-5\Leftrightarrow x=\dfrac{2}{3}\)
\(C=5-\left(2x-1\right)^4\)
Ta có: \(\left(2x-1\right)^4\ge0\forall x\Rightarrow-\left(2x-1\right)^4\le0\forall x\Rightarrow5-\left(2x-1\right)^4\le5\Rightarrow C\le5\)
\(C_{max}=5\Leftrightarrow x=\dfrac{1}{2}\)
\(D=-3\left(x-3\right)^2-\left(y-1\right)^2-2021\)
Ta có: \(\left\{{}\begin{matrix}-3\left(x-3\right)^2\le0\forall x\\-\left(y-1\right)^2\le0\forall y\end{matrix}\right.\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2\le0\forall x,y\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2-2021\le-2021\Rightarrow D\le-2021\)
\(D_{max}=-2021\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
\(E=-\left|x^2-1\right|-\left(x-1\right)^2-y^2-2020\)
\(=-\left|\left(x-1\right)\left(x+1\right)\right|-\left(x-1\right)^2-y^2-2020\)
Ta có: \(\left\{{}\begin{matrix}\left|\left(x-1\right)\left(x+1\right)\right|\ge0\forall x\Rightarrow-\left|\left(x-1\right)\left(x+1\right)\right|\le0\\\left(x-1\right)^2\ge0\forall x\Rightarrow-\left(x-1\right)^2\le0\\y^2\ge0\Rightarrow-y^2\le0\end{matrix}\right.\Rightarrow E\le-2020\)
\(E_{max}=-2020\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)