
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự


\(x^4-2x^3+3x^2-4x+2005=\left(x^4-2x^3+x^2\right)+2\left(x^2-2x+1\right)+2003=\left(x^2-x\right)^2+2\left(x-1\right)^2+2003\)
Vì \(\left(x^2-x\right)^2\ge0\forall x,\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow x^4-2x^3+3x^2-4x+2005\ge0+0+2013=2013\)
\(ĐTXR\Leftrightarrow x=1\)

\(5x^2-6x+9\)
\(=5\left(x^2-\frac{6}{5}x+\frac{9}{5}\right)\)
\(=5\left(x^2-2.x.\frac{3}{5}+\frac{9}{25}+\frac{36}{25}\right)\)
\(=\frac{35}{5}+5\left(x-\frac{3}{5}\right)^2\ge\frac{35}{5}\)
Min \(=\frac{35}{5}\Leftrightarrow x-\frac{3}{5}=0\Rightarrow x=\frac{3}{5}\)

Lời giải:
$A=2x^2+y^2+2xy+2x-2y+2023$
$=(x^2+2xy+y^2)+x^2+2x-2y+2023$
$=(x+y)^2-2(x+y)+x^2+4x+2023$
$=(x+y)^2-2(x+y)+1+(x^2+4x+4)+2018$
$=(x+y-1)^2+(x+2)^2+2018\geq 0+0+2018=2018$
Vậy GTNN của $A$ là $2018$. Giá trị này đạt tại $x+y-1=x+2=0$
$\Leftrightarrow x=-2; y=3$
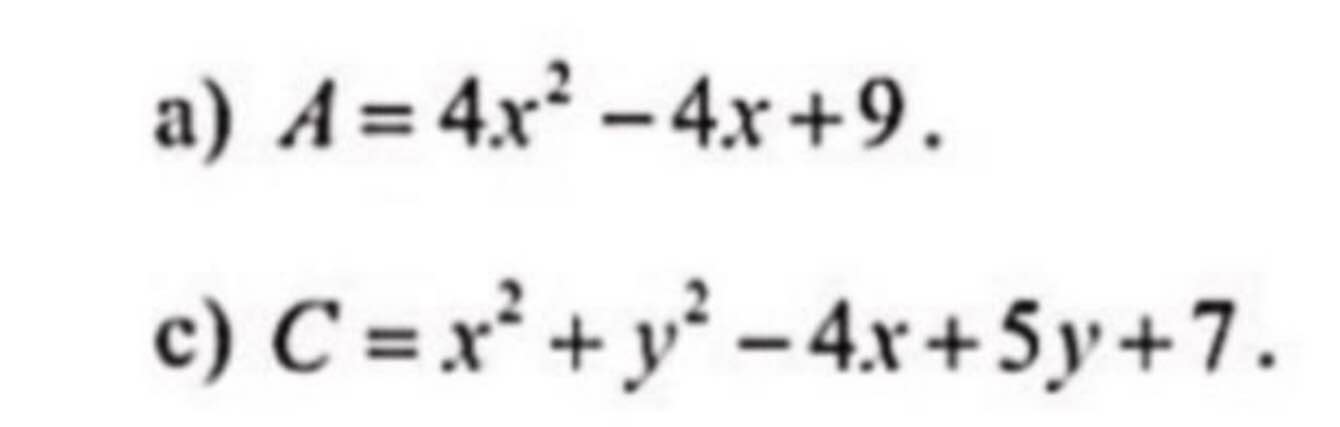

a) \(A=4x^2-4x+9=\left(4x^2-4x+1\right)+8\)
\(=\left(2x-1\right)^2+8\ge8\)
\(minA=8\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=\left(x^2-4x+4\right)+\left(y^2+5y+\dfrac{25}{4}\right)-\dfrac{13}{4}\)
\(=\left(x-2\right)^2+\left(y+\dfrac{5}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\)
\(minC=-\dfrac{13}{4}\Leftrightarrow\) \(\left\{{}\begin{matrix}x=2\\y=-\dfrac{5}{2}\end{matrix}\right.\)