Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x-y=-30\Rightarrow\dfrac{x}{-30}=\dfrac{1}{y}\\ y.z=-42\\ \Rightarrow\dfrac{z}{-42}=\dfrac{1}{y}\\ \Rightarrow\dfrac{x}{-30}=\dfrac{z}{-42}\)
Áp dụng TCDTSBN ta có:
\(\dfrac{x}{-30}=\dfrac{z}{-42}=\dfrac{z-x}{-42-\left(-30\right)}=\dfrac{-12}{-12}=1\)
\(\dfrac{x}{-30}=1\Rightarrow x=-30\\ \dfrac{z}{-42}=1\Rightarrow z=-42\)
\(x.y=-30\Rightarrow-30.y=-30\Rightarrow y=1\)

\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}\) và \(x-3y=20\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{5}=\dfrac{3y}{9}=\dfrac{z}{2}=\dfrac{x-3y}{5-9}=\dfrac{20}{-4}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=-5< =>x=-25\\\dfrac{y}{3}=-5< =>y=-15\\\dfrac{z}{2}=-5< =>z=-10\end{matrix}\right.\)
Vậy ....

Ta có: \(\left(x-\dfrac{1}{5}\right)^{2004}\ge0\forall x\)
\(\left(y+0.4\right)^{100}\ge0\forall y\)
\(\left(z-3\right)^{678}\ge0\forall z\)
Do đó: \(\left(x-\dfrac{1}{5}\right)^{2004}+\left(y+0.4\right)^{100}+\left(z-3\right)^{678}\ge0\forall x,y,z\)
Dấu '=' xảy ra khi
\(\left\{{}\begin{matrix}x-\dfrac{1}{5}=0\\y+0.4=0\\z-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=-\dfrac{2}{5}\\z=3\end{matrix}\right.\)
Vậy: (x,y,z)=\(\left(\dfrac{1}{5};-\dfrac{2}{5};3\right)\)

Bài 1:
Giải:
Vì đại lượng x tỉ lệ nghịch với đại lượng y nên ta có:
\(3x=4y\Rightarrow\frac{x}{4}=\frac{y}{3}\) và \(x+y=14\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x}{4}=\frac{y}{3}=\frac{x+y}{4+3}=\frac{14}{7}=2\)
+) \(\frac{x}{4}=2\Rightarrow x=8\)
+) \(\frac{y}{3}=2\Rightarrow y=6\)
Vậy cặp số \(\left(x;y\right)\) là \(\left(8;6\right)\)
Bài 2:
Giải:
Vì x và y là 2 đại lượng tỉ lệ nghịch nên ta có:
\(6x=8y\Rightarrow\frac{x}{8}=\frac{y}{6}\) và \(2x-3y=10\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x}{8}=\frac{y}{6}=\frac{2x}{16}=\frac{3y}{18}=\frac{2x-3y}{16-18}=\frac{10}{-2}=-5\)
+) \(\frac{x}{8}=-5\Rightarrow x=-40\)
+) \(\frac{y}{6}=-5\Rightarrow y=-30\)
Vậy cặp số \(\left(x;y\right)\) là \(\left(-40;-30\right)\)
1/ Ta có: x;y tỉ lệ nghịch với 3,4
=> \(\frac{\frac{x}{1}}{3}\)=\(\frac{\frac{y}{1}}{4}\) và x+y = 14
Áp dụng tính chất dãy tỉ số bằng nhau, Ta có:
\(\frac{\frac{x}{1}}{3}\)=\(\frac{\frac{y}{1}}{4}\)=\(\frac{x+y}{\frac{1}{3}+\frac{1}{4}}\)=\(\frac{\frac{14}{7}}{12}\)=24
\(\frac{\frac{x}{1}}{3}\)=24 => x = 8
\(\frac{\frac{y}{1}}{4}\)=24 => y = 6
Vậy x = 8 ; y =6
2/ Ta có: x;y tỉ lệ nghịch với 6;8
=> \(\frac{\frac{x}{1}}{6}\)=\(\frac{\frac{y}{1}}{8}\) và 2x-3y = 10
Áp dụng tính chất dãy tỉ số bằng nhau:
Ta có: \(\frac{\frac{x}{1}}{6}\)=\(\frac{\frac{y}{1}}{8}\)=\(\frac{2x-3y}{2.\frac{1}{6}-3.\frac{1}{8}}\)=\(\frac{\frac{10}{-1}}{24}\)=\(\frac{-5}{12}\)
\(\frac{\frac{x}{1}}{6}\)=\(\frac{-5}{12}\)=> x = \(\frac{-5}{72}\)
\(\frac{\frac{y}{1}}{8}\)=\(\frac{-5}{12}\)=> y = \(\frac{-5}{96}\)
Vậy x= \(\frac{-5}{72}\)
y = \(\frac{-5}{96}\)

Áp dụng dãy tỉ số bằng nhau:
b.
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.\left(-1\right)=-2\\y=-5.\left(-1\right)=5\end{matrix}\right.\)
d.
\(\dfrac{4}{x}=\dfrac{7}{y}\Rightarrow\dfrac{y}{7}=\dfrac{x}{4}=\dfrac{y-x}{7-4}=\dfrac{-12}{3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=4.\left(-4\right)=-16\\y=7.\left(-4\right)=-28\end{matrix}\right.\)

a) Ta có: \(x:2=y:\left(-5\right)\)
nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)
mà x-y=-7
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(-2;5)
b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)
nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)
Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x+y-z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(16;24;30)
b)
Do đó ta có
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

a, \(\overline{20x5}\) \(⋮\) 9 ⇔ 2 + 0 + 5 + \(x\) ⋮ 9 ⇔ \(x\) + 2 ⋮ 9 ⇒ \(x\) = 7
Vậy \(x=7\)
b, \(\overline{x998y}\) \(⋮\) 2; 3 và 5
\(\overline{x998y}\) \(⋮\) 2 và 5 ⇔ \(y\) = 0
\(\overline{x998y}\) \(⋮\) 3 ⇔ \(x+9+9+8\) +y ⋮ 3 ⇒ \(x\) + 2 ⋮ 3 ⇒ \(x\) = 1; 4; 7
Vậy các cặp \(x;y\) thỏa mãn đề bài lần lượt là:
(\(x;y\)) =(1; 0); (4; 0); (7; 0)
c, \(\overline{87xy}\) \(⋮\) 9 ⇔ 8 + 7 + \(x+y\) ⋮ 9 ⇒ \(x+y\) + 6 ⋮ 9
\(x-y=4\) ⇒ \(x=4+y\). Thay \(x\) = 4 + y vào biểu thức \(x+y+6\)⋮9
ta có: 4+\(y+y\) +6 \(⋮\) 9 ⇒ 1 + 2⋮ 9 ⇒ 2\(y\) = 8⇒ y =4; \(x\) = 4+4 =8
Vậy \(x=8;y=4\)
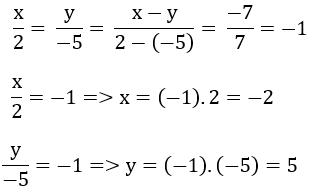
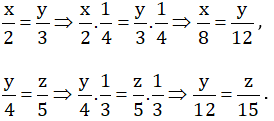
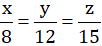
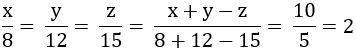
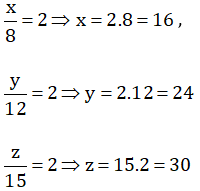
\(\dfrac{x}{-3}=\dfrac{y}{5}=\dfrac{x-y}{-3-5}=\dfrac{-16}{-8}=2\)
\(\dfrac{x}{-3}=2\rightarrow x=-6\\ \dfrac{y}{5}=2\rightarrow y=10\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{-3}=\dfrac{y}{5}=\dfrac{x-y}{-3-5}=\dfrac{-16}{-8}=2\)
Do đó: x=-6; y=10