Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-3\right)=0\)
\(\Leftrightarrow4m^2+4m+1-4m^2+12=0\)
=>4m=-13
hay m=-13/4
c: \(\Leftrightarrow\left(2m-2\right)^2-4m^2>=0\)
\(\Leftrightarrow4m^2-8m+4-4m^2>=0\)
=>-8m>=-4
hay m<=1/2

a: \(\text{Δ}=\left(-5\right)^2-4\left(-2m+5\right)\)
=25+8m-20=8m+5
Để phương trình có nghiệm kép thì 8m+5=0
=>m=-5/8
=>x^2-5x+25/4=0
=>x=5/2
b: \(\text{Δ}=\left(2m-1\right)^2-4\left(m^2-2m+3\right)\)
\(=4m^2-4m+1-4m^2+8m-12=4m-11\)
Để phương trình có nghiệm kép thì 4m-11=0
=>m=11/4
=>x^2-9/2x+81/16=0
=>x=9/4
c: TH1: m=-3
=>-(2*(-3)+1)x+(-3-1)=0
=>-(-5x)-4=0
=>5x-4=0
=>x=4/5(nhận)
TH2: m<>-3
\(\text{Δ}=\left(2m+1\right)^2-4\left(m+3\right)\left(m-1\right)\)
\(=4m^2+4m+1-4\left(m^2+2m-3\right)\)
\(=4m^2+4m+1-4m^2-8m+12=-4m+13\)
Để phương trình có nghiệm kép thì -4m+13=0
=>m=13/4
=>25/4x^2-15/2x+9/4=0
=>(5/2x-3/2)^2=0
=>x=3/2:5/2=3/2*2/5=3/5

b) Thay x=2 vào pt, ta được:
\(4\left(m^2-1\right)-4m+m^2+m+4=0\)
\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)
\(\Leftrightarrow5m^2-3m=0\)
\(\Leftrightarrow m\left(5m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=\dfrac{2m}{m^2-1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)

câu a
Gọi x0 là nghiệm chung của PT(1) và (2)
\(\Rightarrow\left\{{}\begin{matrix}2x^2_0+\left(3m-1\right)x_0-3=0\left(\times3\right)\\6.x^2_0-\left(2m-1\right)x_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x^2_0+3\left(3m-1\right)x_0-9=0\left(1\right)\\6x^2_0-\left(2m-1\right)x_0-1=0\left(2\right)\end{matrix}\right.\) Lấy (1)-(2) ,ta được
PT\(\Leftrightarrow3\left(3m-1\right)-9+\left(2m-1\right)+1\)=0
\(\Leftrightarrow9m-3-9+2m-1+1=0\Leftrightarrow11m-12=0\)
\(\Leftrightarrow m=\dfrac{12}{11}\)

1:
\(=\left(\dfrac{1}{x-2\sqrt{x}}+\dfrac{2}{3\sqrt{x}-6}\right):\dfrac{2\sqrt{x}+3}{3\sqrt{x}}\)
\(=\dfrac{3+2\sqrt{x}}{3\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{3\sqrt{x}}{2\sqrt{x}+3}=\dfrac{1}{\sqrt{x}-2}\)
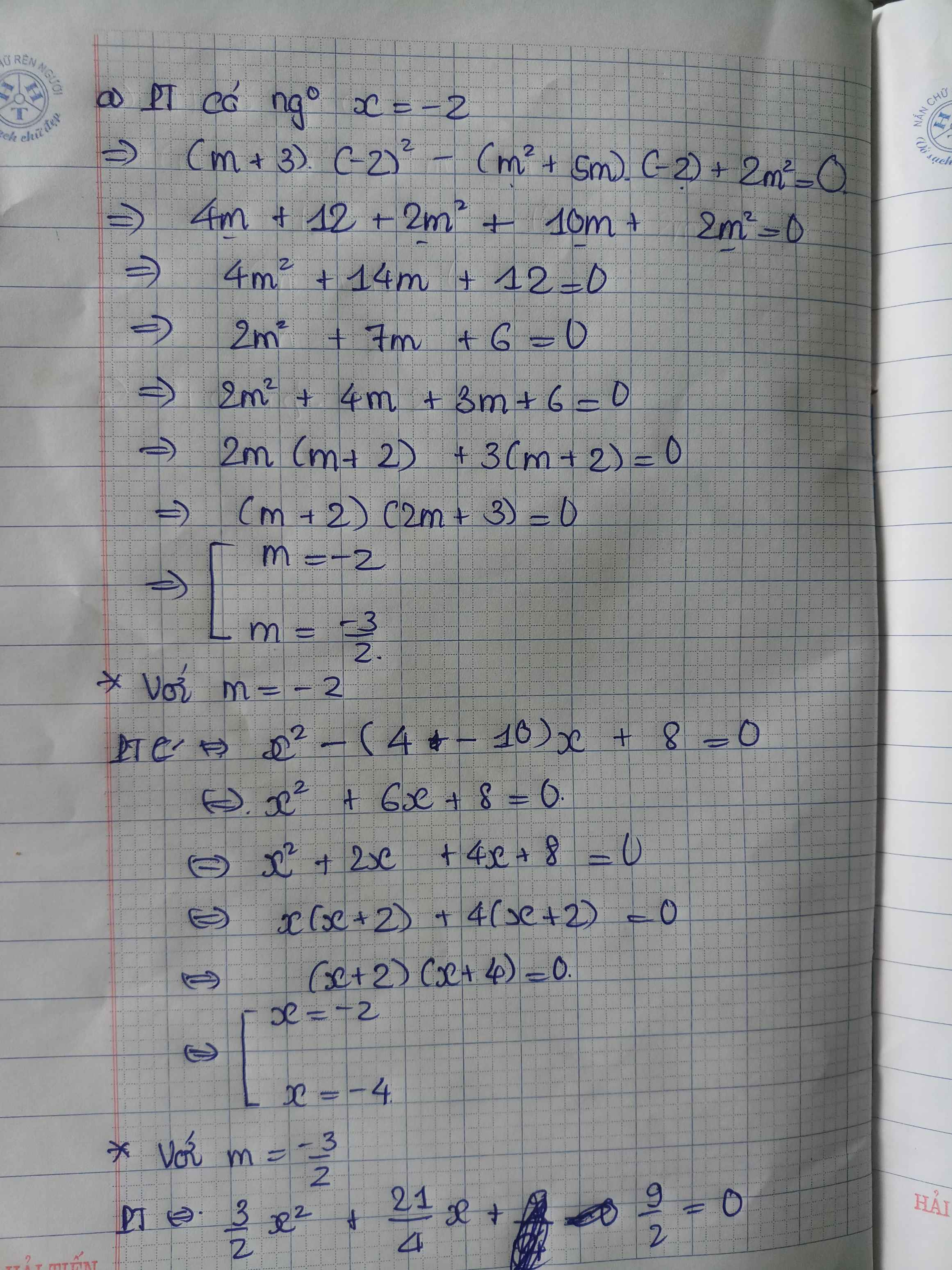
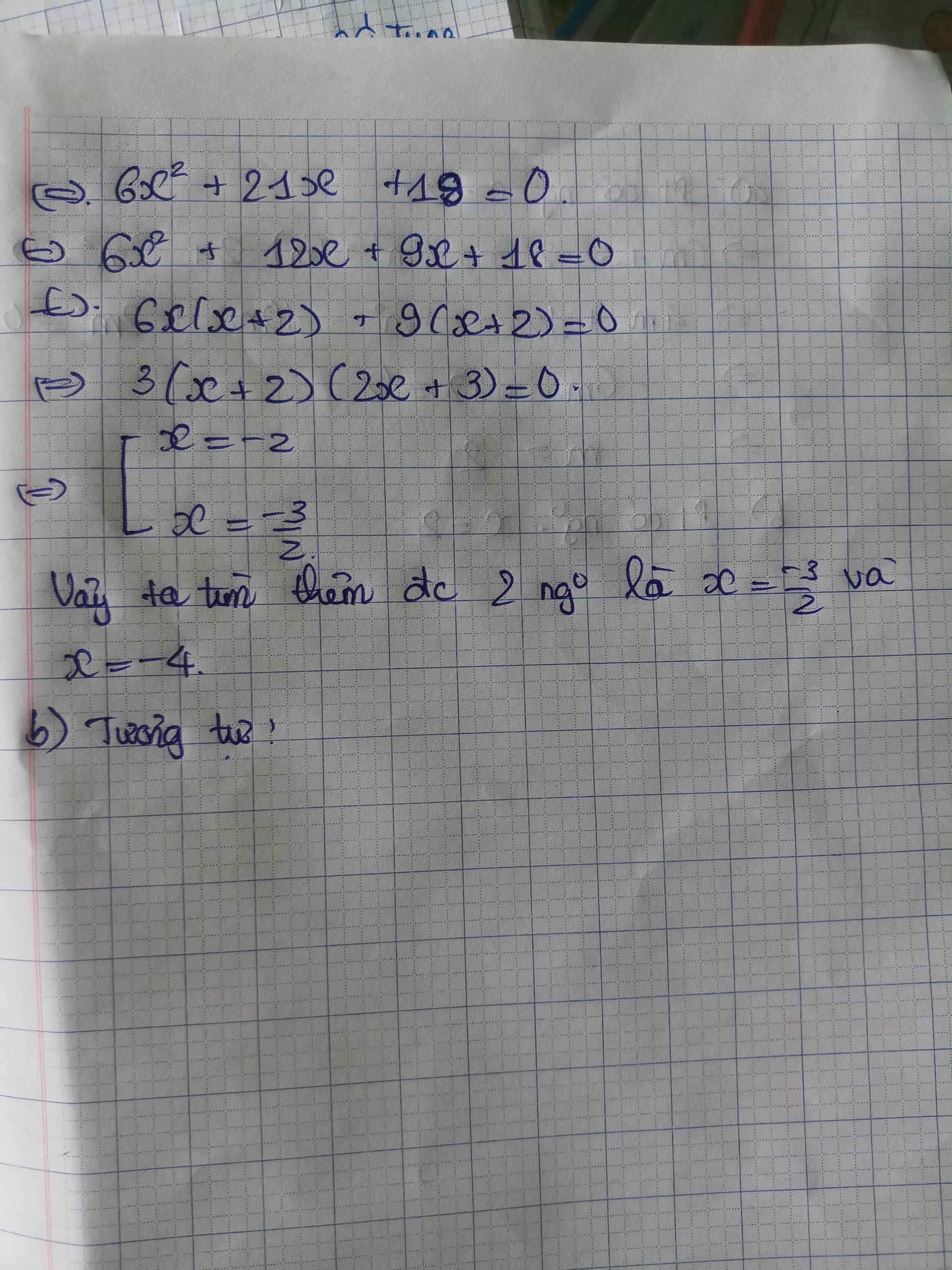
a: \(\Leftrightarrow\left(2m-4\right)^2-4\left(m^2-3\right)>=0\)
\(\Leftrightarrow4m^2-16m+16-4m^2+12>=0\)
=>-16m>=-28
hay m<=7/4
b: \(\Leftrightarrow16m^2-4\left(2m-1\right)\left(2m+3\right)=0\)
\(\Leftrightarrow16m^2-4\left(4m^2+4m-3\right)=0\)
=>4m-3=0
hay m=3/4
c: \(\Leftrightarrow\left(4m-2\right)^2-4\cdot4\cdot m^2< 0\)
=>-16m+4<0
hay m>1/4