
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LH
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
30 tháng 3 2017
Đáp án D
Đặt t = 3sin x - 4cos x => -5 ≤ t ≤ 5 (dùng bất đẳng thức bunhiacopxki)
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 2)2 -1
Do -5 ≤ t ≤ 5 => 0 ≤ (t – 2)2 ≤ 36 => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.

NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
\(\Leftrightarrow2cos^2x+4cosx-1=-m\)
Xét \(f\left(x\right)=2cos^2x+4cosx-1\)
\(f\left(x\right)=2cos^2x+4cosx+2-3=2\left(cosx+1\right)^2-3\ge-3\)
\(f\left(x\right)=2cos^2x+4cosx-6+5=2\left(cosx-1\right)\left(cosx+3\right)+5\le5\)
\(\Rightarrow-3\le-m\le5\Rightarrow-5\le m\le3\)
MM
0

H
0

PT
1
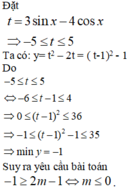
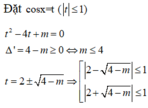

ĐKXĐ: \(cosx\ne\frac{3}{4}\)
\(\Leftrightarrow3sinx+m=8cosx-6\)
\(\Leftrightarrow3sinx-8cosx=-m-6\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(3^2+8^2\ge\left(-m-6\right)^2\)
\(\Rightarrow\left(m+6\right)^2\le73\)
\(\Rightarrow-6-\sqrt{73}\le m\le-6+\sqrt{73}\)
Kết hợp thêm điều kiện \(m\ne12\pm\frac{3\sqrt{7}}{4}\)