Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Đặt $2^x=t$ thì pt trở thành:
$t^2-2mt+2m=0(*)$
Ta cần tìm $m$ để pt $(*)$ có hai nghiệm $t>0$ phân biệt thỏa mãn $t_1t_2=4$
$(*)$ có 2 nghiệm thì:
$\Delta'=m^2-2m>0\Leftrightarrow m(m-2)>0\Leftrightarrow m>2$ hoặc $m<0$ (1)
Áp dụng định lý Viet, để $(*)$ có 2 nghiệm dương thỏa mãn tích 2 nghiệm bằng 4 thì:
\(\left\{\begin{matrix} S=t_1+t_2>0\\ P=t_1t_2=4\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2m>0\\ 2m=4\end{matrix}\right.\Leftrightarrow m=2\) (2)
Từ $(1); (2)\Rightarrow$ không có giá trị nào của $m$ thỏa mãn

\(\Leftrightarrow\left\{{}\begin{matrix}3.2^xlogx-12logx-2^x+4=0\left(1\right)\\5^x=m\left(2\right)\end{matrix}\right.\) và \(5^x\ge m\) (\(x>0\))
Xét (1):
\(\Leftrightarrow3logx\left(2^x-4\right)-\left(2^x-4\right)=0\)
\(\Leftrightarrow\left(3logx-1\right)\left(2^x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=\sqrt[3]{10}\end{matrix}\right.\)
\(y=5^x\) đồng biến trên R nên (2) có tối đa 1 nghiệm
Để pt đã cho có đúng 2 nghiệm phân biệt ta có các TH sau:
TH1: (2) vô nghiệm \(\Rightarrow m\le0\) (ko có số nguyên dương nào)
TH2: (2) có nghiệm (khác với 2 nghiệm của (1)), đồng thời giá trị của m khiến cho đúng 1 nghiệm của (1) nằm ngoài miền xác định
(2) có nghiệm \(\Rightarrow m>0\Rightarrow x_3=log_5m\)
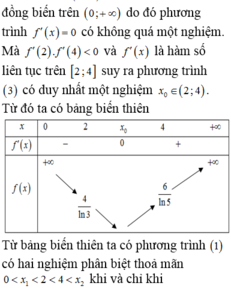
Do \(\sqrt[3]{10}>2\) nên bài toán thỏa mãn khi: \(x_1< x_3< x_2\)
\(\Rightarrow2< log_5m< \sqrt[3]{10}\)
\(\Rightarrow25< m< 5^{\sqrt[3]{10}}\) (hơn 32 chút xíu)
\(\Rightarrow\) \(32-26+1\) giá trị nguyên
tìm m để phương trình \(7x^3+\left(2m-9\right)x^2-\left(m^2+2m-2\right)x-2=0\) có 3 nghiệm phân biệt


ĐKXĐ: \(x>0\)
\(x^{log_25}=t\Rightarrow25^{log_2x}=\left(5^{log_2x}\right)^2=\left(x^{log_25}\right)^2=t^2\)
\(x_1x_2=4\Rightarrow t_1t_2=\left(x_1x_2\right)^{log_25}=4^{log_25}=25\)
\(\left(m+1\right)t^2+\left(m-2\right)t-2m+1=0\) (1)
Pt có 2 nghiệm pb \(\Rightarrow\) (1) có 2 nghiệm dương pb
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-2\right)^2-4\left(m+1\right)\left(-2m+1\right)>0\\t_1+t_2=\dfrac{2-m}{m+1}>0\\t_1t_2=\dfrac{-2m+1}{m+1}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\-1< m< \dfrac{1}{2}\end{matrix}\right.\)
Ủa làm đến đây mới thấy kì kì, chỉ riêng hệ điều kiện này đã ko tồn tại m nguyên rồi, chưa cần điều kiện \(x_1x_2=4\)
cái này mk làm 1 nghiệm t =1 xong thay tìm m, có vẻ cũng ko dài lắm :))))

\(f\left(1-x\right)+f\left(x\right)=\dfrac{9^{1-x}}{9^{1-x}+3}+\dfrac{9^x}{9^x+3}=\dfrac{9}{9+3.9^x}+\dfrac{9^x}{9^x+3}=\dfrac{3}{9^x+3}+\dfrac{9^x}{9^x+3}=1\)
\(\Rightarrow f\left(x\right)=1-f\left(1-x\right)\)
\(\Rightarrow f\left(cos^2x\right)=1-f\left(sin^2x\right)\)
Do đó:
\(f\left(3m+\dfrac{1}{4}sinx\right)+f\left(cos^2x\right)=1\)
\(\Leftrightarrow f\left(3m+\dfrac{1}{4}sinx\right)=f\left(sin^2x\right)\) (1)
Hàm \(f\left(x\right)=\dfrac{9^x}{9^x+3}\) có \(f'\left(x\right)=\dfrac{3.9^x.ln9}{\left(9^x+3\right)^2}>0\Rightarrow f\left(x\right)\) đồng biến trên R
\(\Rightarrow\left(1\right)\Leftrightarrow3m+\dfrac{1}{4}sinx=sin^2x\)
Đến đây chắc dễ rồi, biện luận để pt \(sin^2x-\dfrac{1}{4}sinx=3m\) có 8 nghiệm trên khoảng đã cho


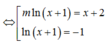
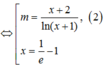

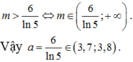


Đáp án D
Bước 1: Ta giữ nguyên phần đồ thị phía trên trục hoành.
Bước 2: Lấy đối xứng phần phía dưới trục hoành của đồ thị lên phía trên trục hoành và xóa bỏ đi phần đồ thị nằm phía dưới trục hoành ta được đồ thị hàm số y = x 4 - 5 x 2 + 4
Khi đó số nghiệm của phương trình x 4 - 5 x 2 + 4 = log 2 m chính là số giao điểm của đồ thị hàm số y = x 4 - 5 x 2 + 4 và đường thẳng y = log 2 m với m > 0.Dựa vào đồ thị hàm số y = x 4 - 5 x 2 + 4 ta thấy để phương trình x 4 - 5 x 2 + 4 = log 2 m có 8 nghiệm thì: 0 < log 2 m < 9 4 ⇔ 1 < m < 2 9 4