
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=1-\frac{4}{x}+\frac{1}{x^2}=\left(4-\frac{4}{x}+\frac{1}{x^2}\right)-3=\left(2-\frac{1}{x}\right)^2-3\)
\(\Rightarrow A\ge-3\)Dấu "=" xảy ra khi \(\left(2-\frac{1}{x}\right)^2=0\Rightarrow\frac{1}{x}=2\Rightarrow x=\frac{1}{2}\)
Vậy GTNN của A=-3 khi \(x=\frac{1}{2}\)

A = (4x + 3)/(x² + 1)
CM bất đẳng thức phụ : (a² + b²)(c² + d²) ≥ (ac + bd)² (1)
Đây là bất đẳng thức bunhiacopxki , nếu em chưa biết thì anh CM luôn :
(1) <=> a²c² + a²d² + b²c² + b²d² ≥ a²c² + 2abcd + b²d²
<=> a²d² - 2.ad.bc + b²c² ≥ 0
<=> (ad - bc)² ≥ 0 --> luôn đúng --> bđt (1) được CM
- Dấu " = " xảy ra <=> ad = bc <=> a/c = b/d
- Áp dụng bđt (1) ta có : (4.x + 3.1)² ≤ (4² + 3²)(x² + 1²)
<=> (4x + 3)² ≤ 25(x² + 1)
<=> -5.√(x² + 1) ≤ 4x + 3 ≤ 5.√(x² + 1)
<=> -5/√(x² + 1) ≤ A = (4x + 3)/(x² + 1) ≤ 5/√(x² + 1)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

A=4x^2-2x+1/x^2
A=3x^2/x^2+x^2-2x+1/x^2
A=3+(x-1)^2/x^2> hoặc bằng 3
Min A=3 tại x=1

a)
\(B=\frac{x^2-4x+1}{x^2}=1-\frac{4}{x}+\frac{1}{x^2}\)
Đặt \(y=\frac{1}{x}\)
\(\Rightarrow B=1-4y+y^2=y^2-4y+4-3=\left(y-2\right)^2-3\ge-3\)
Dấu = xảy ra \(\Leftrightarrow y=2\Leftrightarrow\frac{1}{x}=2\Leftrightarrow x=\frac{1}{2}\)
Vậy GTNN của B là -3 <=> x=1/2
\(C=\frac{2x}{x^2+1}=\frac{x^2+1-x^2+2x-1}{x^2+1}=1-\frac{\left(x-1\right)^2}{x^2+1}\le1\)
Dấu bằng xảy ra <=> x=1
\(C=\frac{2x}{x^2+1}=\frac{x^2+2x+1-x^2-1}{x^2+1}=\frac{\left(x+1\right)^2}{x^2+1}-1\ge-1\)
Dấu bằng xảy ra <=> x=-1
Vậy maxC=1 <=>x=1
minC=-1 <=> x=-1

A=\(\frac{2\left(x^2-8x+22\right)-1}{x^2-8x+22}\)=2-\(\frac{1}{x^2-8x+22}\)
ĐỂ A CÓ GTNH THÌ \(\frac{1}{x^2-8x+22}\)LỚN NHẤt thì x2-8x+22 nhỏ nhất
SUY RA X2-8X+22=x2-8x+16+6=(x-4)2+6>=6(do (x-4)2>=0)
GTNN CỦA x2-8x+22 là 6 khi và chỉ khi (x-4)2=0\(\Leftrightarrow\)x=4
vậy GTNN CỦA A=2-\(\frac{1}{6}\)=\(\frac{11}{6}\)TẠI X=4
B=1-\(\frac{4}{x}\)+\(\frac{1}{x^2}\)
Dặt \(\frac{1}{x}\)=t ta có
B=1-4t+t2=t2-4t+4-3=(t-2)2-3>=-3 dấu bằng xảy ra khi và chỉ khi (t-2)2=0\(\Leftrightarrow\)t=2
\(\Leftrightarrow\)\(\frac{1}{x}\)=2
\(\Leftrightarrow\)=\(\frac{1}{2}\)
vậy GTNN là -3 tại x=1/2
2,a, GTNN A=\(\frac{x^2-12x+36-x^2-9}{x^2+9}\)=\(\frac{\left(x-6\right)^2-\left(x^2+9\right)}{x^2+9}\)=\(\frac{\left(x-6\right)^2}{x^2+9}\)-1
do \(\frac{\left(x-6\right)^2}{x^2+9}\)\(\ge\)0 với mọi x \(\Rightarrow\)\(\frac{\left(x-6\right)^2}{x^2+9}\)-1\(\ge\)-1
dấu = xảy ra khi và chỉ khi (x-6)2\(\Leftrightarrow\)x=6
vậy GTNN của A=-1 tại x=6
B,GTNN B=\(\frac{4\left(x^2+2x+1\right)-4x^2-1}{4x^2+1}\)=\(\frac{4\left(x+1\right)^2}{4x^2+1}\)-1
DO \(\frac{4\left(x+1\right)^2}{4x^2+1}\)\(\ge\)0\(\Rightarrow\)\(\frac{4\left(x+1\right)^2}{4x^2+1}\)-1\(\ge\)-1
dấu =xảy ra khi và chỉ khi 4(x+1)2=0
\(\Leftrightarrow\)x=-1
vạy GTNN của B=-1 tại x=-1
C, GTLN C=\(\frac{-\left(x^2-2x+1\right)+x^2+2}{x^2+2}\)=2-\(\frac{\left(x-1\right)^2}{x^2+2}\)
DO \(\frac{\left(x-1\right)^2}{x^2+2}\)\(\ge\)0\(\Rightarrow\) 2- \(\frac{\left(x-1\right)^2}{x^2+2}\)\(\le\)2
dấu = xảy ra khi và chỉ khi (x-1)2=0\(\Leftrightarrow\)x=1
Vậy GTLN của c=2 tại x=1

\(A=\frac{4x^2-4x+1-3x^2}{x^2}=\left(\frac{2x-1}{x}\right)^2-3\ge-3\)
Dấu "=" xảy ra <=> x = 1/2
Vậy min A = -3 đạt tại x = 1/2

1.a) Không tồn tại\(\)
b) 1997 tại x=4
c) 4 tại x=1;y=2
d) 164 tại x=8
2.a) x>3 và x<-1
b) Không tốn tại x
Câu 1: Hoàn thành các phương trình phản ứng sau: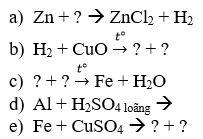
Câu 2: Hãy xác định chất oxi hóa, chất khử, sự oxi hóa và sự khử trong phản ứng oxi hóa – khử sau:
H2 + HgO −to→ Hg + H2O
Câu 3: Có 3 lọ đựng riêng biệt các khí sau: oxi, không khí và hiđro. Bằng thí nghiệm nào có thể nhận ra các khí trong mỗi lọ?
Câu 4: Lập phương trình hóa học cho các phản ứng sau:
Cacbon đioxit + nước →axit cacbonic (H2CO3)
Lưu huỳnh đioxit + nước → axit sunfurơ (H2SO3)
Sắt + axit clohidric → sắt clorua + H2↑
Điphotpho pentaoxit + nước → axit photphoric (H3PO4)
Chì(II) oxit + hiđro→chì (Pb) + nước
Câu 5: Trong phòng thí nghiệm, người ta dùng hiđro để khử sắt(III) oxit và thu được 11,2 gam sắt.
Viết phản ứng hóa học xảy ra.
Tính khối lượng sắt(III) oxit đã phản ứng.
Tính thể tích khí hiđro đã tiêu thụ (đktc).
Đáp án và hướng dẫn giải
Câu 1:Hoàn thành các phương trình phản ứng: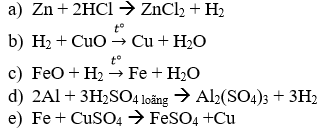
Câu 2: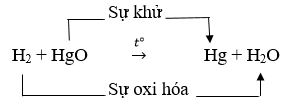
Câu 3: Đưa que đóm còn tàn đóm đỏ vào 3 bình khí trên. Bình khí làm que đóm bùng cháy là oxi.
Đốt 2 khí còn lại. Khi cháy với ngọn lửa màu xanh nhạt là H2, còn lại là không khí.
2H2 + O2 → 2H2O
Câu 4: Lập phương trình các phản ứng:
Cacbon đioxit + nước → axit cacbonic (H2CO3)
CO2 + H2O → HCO3
Lưu huỳnh đioxit + nước → axit sunfurơ (H2SO3)
SO2 + H2O →H2SO3
Sắt + axit clohiđric → sắt clorua + H2 ↑
Fe + 2HCl → FeCl2 + H2
Điphotpho pentaoxit + nước → axit photphoric (H3PO4)
P2O5 + 3H2O → H3PO4
Chì(II) oxit + hiđro → chì (Pb) + nước
PbO + H2 −to→ Pb + H2O
Câu 5:
PTHH:
Fe2O3 + 3H2 −to→ 2Fe + 3H2O (1)
(mol) 0,1 0,3 ← 0,2
Ta có: nFe = 11,2/56 = 0,2 (mol)
Từ (1) → nFe2O3= 0,1 (mol) → mFe2O3= 0,1 x 160 = 16 (gam)
Từ (1) → nH2= 0,3 (mol)
→ VH2= 0,3 x 22,4 = 6,72 (lít)
A= -3x^2 +4x^2-4x+1/ x^2
=-3 + ( 2x+1)^2/x^2
(2x+1)^2/ x^2 >= 0
=> A>= -3
Min A=-3
dấu bằng xảy ra <=> 2x+1 =0 ...