Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
đơn điệu trên R là sao bạn? bạn chỉ mk cách nhận bt đc ko?

\(\left(\frac{2x-1}{x+2}\right)'=\frac{5}{\left(x+2\right)^2}>0\)
Vậy hàm số \(y=\frac{2x-1}{x+2}\) đồng biến trên R. Chọn A.
A. là hàm phân thức bậc nhất trên bậc nhất nên không đồng biến trên \(ℝ\).
B., D. là đa thức, có hệ số cao nhất âm nên cũng không thể đồng biến trên \(ℝ\).
C>: \(\left(x^3+2x+1\right)'=3x^2+2>0,\forall x\inℝ\).
Ta chọn C.

\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.


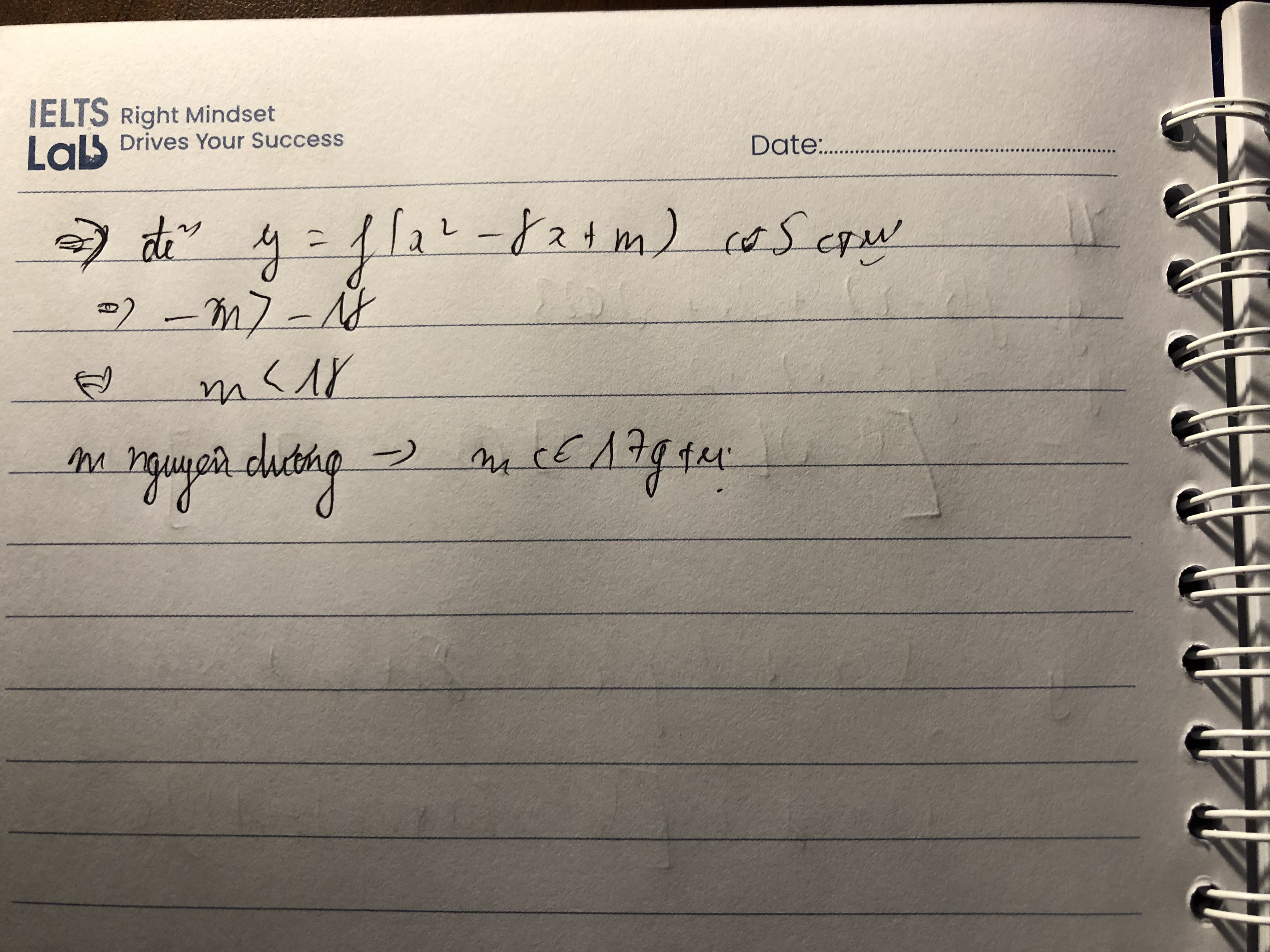
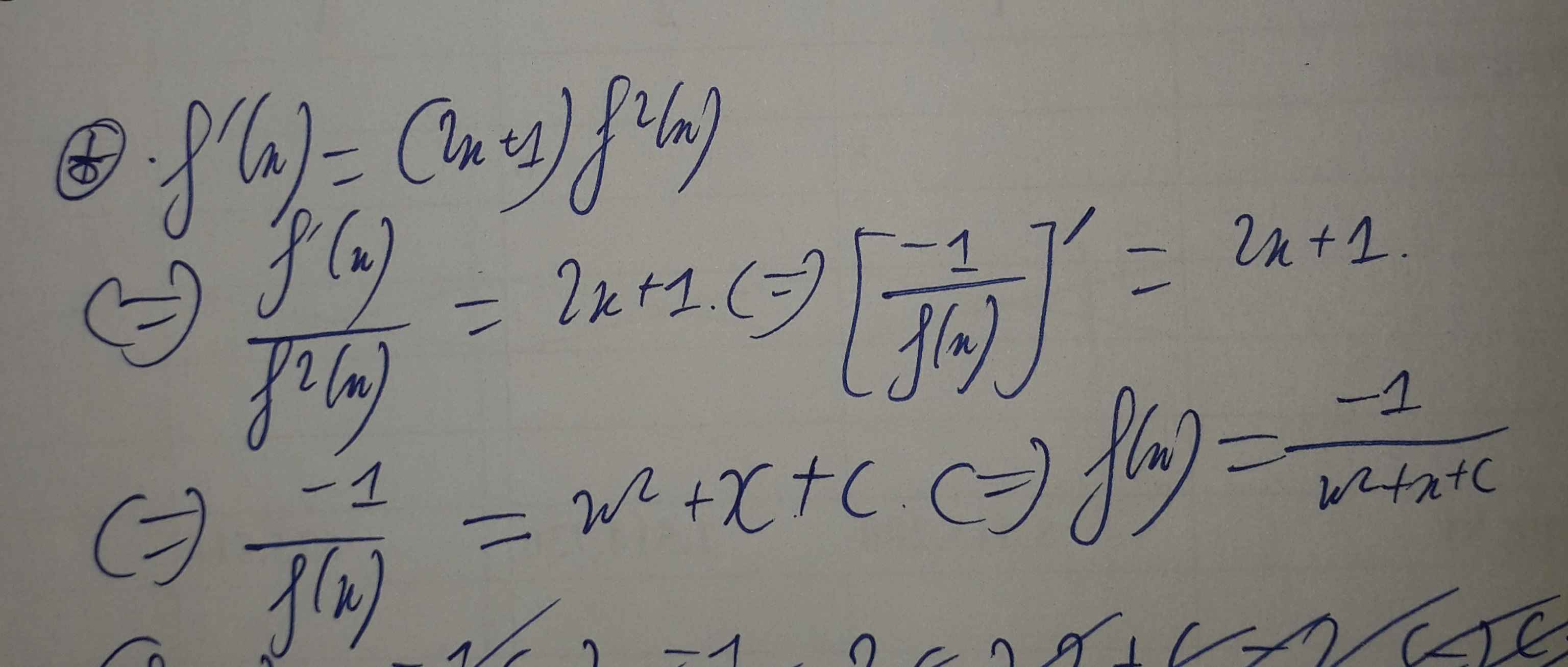
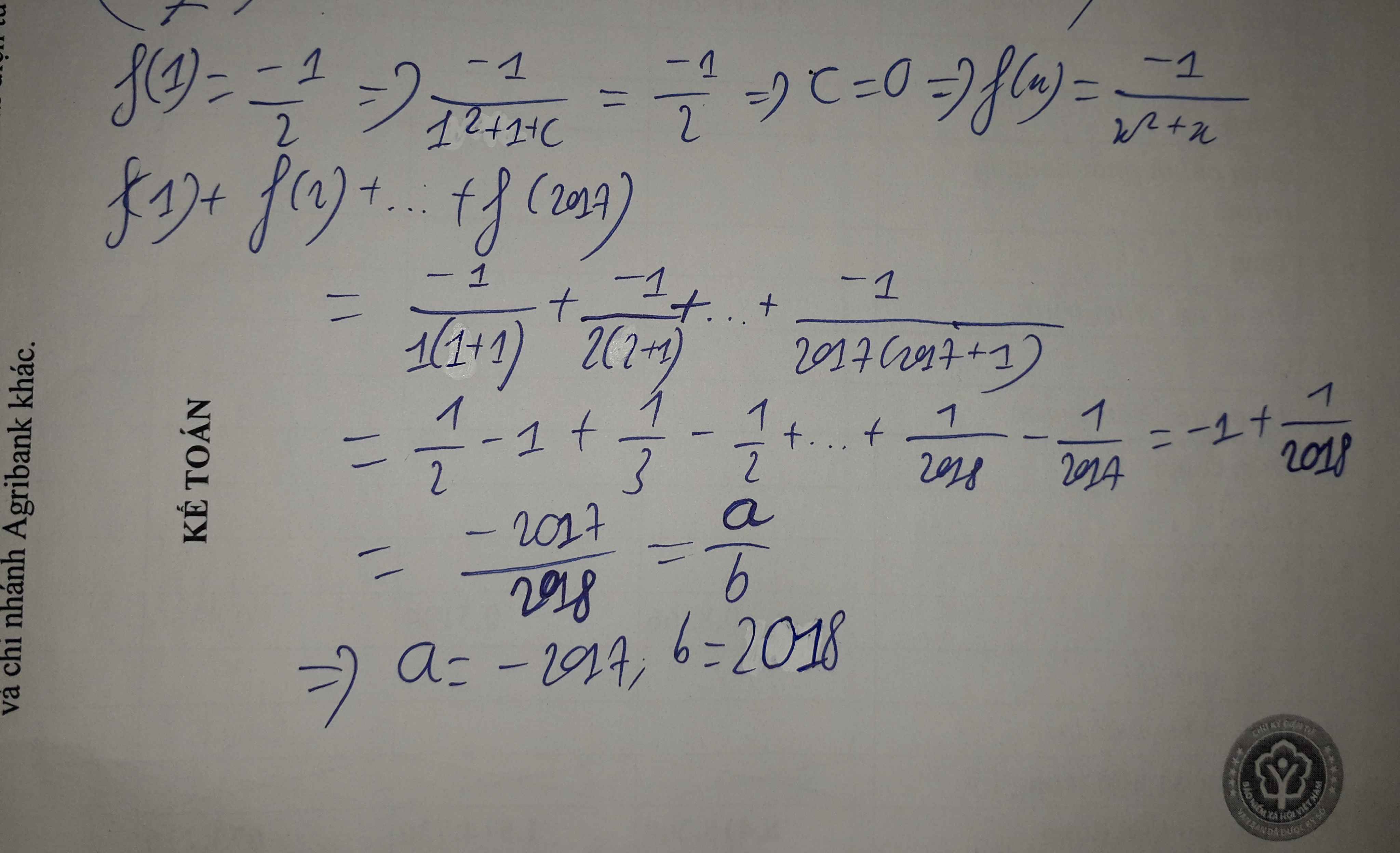
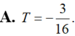
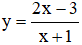
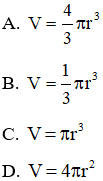
Tập xác định D=R.
Ta có: y’=2+a.cosx-b.sinx
Áp dụng bất đẳng thức Schwartz ta có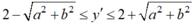
Yêu cầu của bài toán đưa đến giải bất phương trình
Chọn C.