a.

\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)

\(\Rightarrow1-2\left(m-2\right)+m+10=0\)

\(\Rightarrow m=15\)

Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)

b.

Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)

\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)

Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)

Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)

c.

Pt có 2 nghiệm âm pb khi:

\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)

d.

\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\) 

Không tồn tại m thỏa mãn

e cảm ơn ạ

Phương án A có nhiều giá trị quá, thay vào phương trình mất nhiều thời gian, nên ta xét các phương trình còn lại.

Với phương án B, khi thay x = 0 vào phương trình thì hai vế đều bằng 4 nên x = 0 là một nghiệm. Tuy nhiên khi thay giá trị x = 4 vào phương trình thì vế trái bằng 0, còn vế phải bằng 16. Vậy phương án B và phương án C đều bị loại. Với phương án D, giá trị x = 1 cũng không phải là nghiệm của phương trình, nên phương án D bị loại.

Đáp án: A

Điều kiện của phương trình:

4x – 3 ≥ 0 ⇒ x ≥ 3/4;

-2x + 1 ≥0 ⇒ x ≤ 1/2.

Không có giá trị nào của x thỏa mãn hai điều kiện này nên phương trình vô nghiệm.

Đáp án: D

Câu 1: D

Bạn ơi câu 2 đâu

Với giá trị x = 0 thì vế trái của phương trình tương đương, còn vế phải âm nên phương án A và B đều bị loại. Tương tự, với x = -2 thì vế trái dương, vế phải âm nên phương án D bị loại.

Đáp án: C

 Tập nghiệm của bất phương trình đã cho là đoạn [2a - b + 1; -a + 2b - 1] (nếu 2a - 6 + 1 ≤ -a + 26 - 1) hoặc là đoạn [-a + 26 - 1 ; 2a - 6 + 1] (nếu -a + 2b - 1 ≤ 2a - 6 - 1)

    Do đó để tập nghiệm của bất phương trình đã cho là đoạn [0;2], điều kiện cần và đủ là:

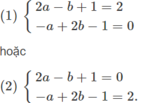
Giải (1) ta được a = b = 1. Giải hệ (2) ta được a = 1/3, b = 5/3

    Đáp số: a = b = 1 hoặc a = 1/3, b = 5/3

a) \(\begin{cases}x^2-5x+6<0\\ax+4<0\end{cases}\)

bất phương trình đầu có nghiệm là 1 < x < 6

Xét a = 0 => bpt thứ hai vô nghiệm (4 < 0) => Hệ vô nghiệm

Xét a > 0 => bpt thứ hai có nghiệm là x < -4/a < 0 => kết hợp với 1 < x < 6 thì hệ vô nghiệm

Xét a < 0 => bpt thứ hai có nghiệm là x > -4/a. Kết hợp với 1 < x < 6 thì để hệ có nghiệm thì -4/a <6 => -4 > 6a => a < -4/6 = -2/3, thỏa mãn đk a <0

ĐS: a < -2/3

b) bpt thứ nhất có nghiệm là x > 1.

bpt thứ hai có dạng: (x - a)² +1 - a² < 0; (x - a)² < a² - 1

Nếu a² - 1 < 0, tức là -1 < a < 1 thì bpt trên vô nghiệm,

Nếu a < -1 hoặc a > 1 thì bpt trên có nghiệm là \(-\sqrt{a^2-1}+a\le x\le\sqrt{a^2-1}+a\)

Kết hợp với nghiệm x > 1 thì để hệ có nghieemh ta phải có \(\sqrt{a^2+1}+a>1\) => \(\sqrt{a^2+1}>1-a\), nếu a>1 thì luôn đúng, còn nếu a < -1 thì a² + 1 > 1 - 2a + a² =>a >0 (mâu thuẫn với a < -1)

KL: với a > 1 thì hệ bpt có nghiệm

Đáp án c) nhé em. 

x-2<=0 => x<=2

x²(x-2)<=0 => x=0 hoặc x-2<=0 => x<=2

Em mới học lớp 6 thôi ạ! Xin lỗi nhiều vì không giúp được!