Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thiếu dữ liệu quan trọng nhất là diện tích tam giác bằng bao nhiêu

Do đường thẳng d đi qua điểm I (1; 3) nên a + b = 3 ⇒ a = 3 − b
Giao điểm của d và các tia Ox, Oy lần lượt là M ∈ − b a ; 0 và N 0 ; b
(Với b > 0, a < 0 suy ra b > 3)
Do đó: S Δ O M N = 1 2 . O M . O N = 1 2 . b a . b = b 2 2 a . Mà S Δ O M N = 6 ⇔ b 2 = 12 a
⇔ b 2 = 12 3 − b ⇔ b 2 = 36 − 12 b b 2 = − 36 + 12 b ⇔ b = 6 ( T M ) b = − 6 + 72 ( L ) b = − 6 − 72 ( L )
Với b = 6 ⇒ a = − 3 ⇒ d : y = − 3 x + 6
Đáp án cần chọn là: A

Gọi pt đường thẳng có dạng: \(y=ax+b\)
Đường thẳng qua M nên: \(6=-a+b\Rightarrow b=a+6\)
\(\Rightarrow y=ax+a+6\)
Đường thẳng cắt 2 tia Ox, Oy khi \(a\ne\left\{-6;0\right\}\)
Gọi A là giao điểm với Ox \(\Rightarrow A\left(-\dfrac{a+6}{a};0\right)\) \(\Rightarrow OA=\left|x_A\right|=\left|\dfrac{a+6}{a}\right|\)
Gọi B là giao điểm với Oy \(\Rightarrow B\left(0;a+6\right)\Rightarrow OB=\left|y_B\right|=\left|a+6\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}\left|\dfrac{a+6}{a}\right|.\left|a+6\right|=4\)
\(\Leftrightarrow\left|\dfrac{a^2+12a+36}{a}\right|=8\Rightarrow a^2+20a+36=0\)
\(\Rightarrow\left[{}\begin{matrix}a=-2\\a=-18\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=-2x+4\\y=-18x-12\end{matrix}\right.\)



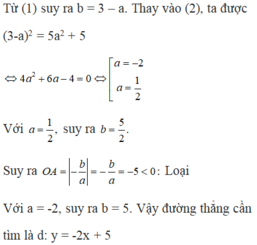
Theo đề ta có : I\(\in\)d \(\Rightarrow\)2=a+b (1)
Lại có d tạo với hai tia Ox, Oy một tam giác diện tích bằng 4
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\text{y}\text{=}b\\x=\frac{-b}{a}\end{matrix}\right.\)
\(\Rightarrow\)S=\(\frac{1}{2}\frac{-b}{a}b=4\Leftrightarrow\frac{-b^2}{8}=a\:\left(2\right)\)
Thay (2) vào (1) ta co: \(b-\frac{b^2}{8}=2\:\Leftrightarrow8b-b^2-16=0\)
\(\Leftrightarrow b=4\:\Rightarrow\:a=-2\)
\(\Rightarrow\)d: y=-2x+4
Suy ra: A=(-2)2+42=20