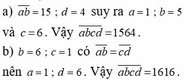abcd +(ab + cd ) =4472

100ab +cd +ab + cd =4472

101ab +2cd =4472

4472 = 101*44+28

=> ab = 44 , 2cd = 28 => cd =14

kl: ab = 44, cd =14

Đúng mình sẽ like nha

có cái nịt :)

ta có 

abcd

= ab. 100 + cd

=8cd . 100 + cd

= cd ( 100.8 + 1)

= cd .801

mà 801 ⋮ 89 

=. cd. 801 ⋮ 89

=> abcd ⋮ 89

\(\overline{abcd}\) = \(\overline{ab}\) x 100 + \(\overline{cd}\) 

Thay \(\overline{ab}\) = 8.\(\overline{cd}\) vào biểu thức: \(\overline{abcd}\) = \(\overline{ab}\) x 100 + \(\overline{cd}\) ta có: 

\(\overline{abcd}\) = 8.\(\overline{cd}\).100 + \(\overline{cd}\)

\(\overline{abcd}\) = 801.\(\overline{cd}\) = 89.9.\(\overline{cd}\) ⋮ 89 (đpcm)

ab là:

(73-35):2=19

cd là:

19+35=74

Năm abcd là:1954

ngày 7 tháng 5 năm 1954

a)  a b c d  = 15; d = 4 suy ra a = 1; b = 5 và c = 6. Vậy  a b c d = 1564.

b) b = 6; c = 1 có  a b = c d nên a = 1; d = 6. Vậy  a b c d = 1616.

(abcd) là kí hiệu số có 4 chữ số abcd. 
từ: (ab)-(cd)=1 => (ab) =1+(cd) 
giả sử n^2 = (abcd) = 100(ab) + (cd) = 100( 1+(cd)) + (cd) = 101(cd) +100  
đk : 31<n<100 
=> 101(cd) = n^2 -100 = (n+10)(n-10) 
vì n< 100 => n-10 < 90 và 101 là số nguyên tố nên: n+10 = 101 => n =91 
thử lại: số chính phương 91^2 = 8281 thỏa đk 82-81=1

(abcd) là kí hiệu số có 4 chữ số abcd.

  từ: (ab)-(cd)=1 => (ab) =1+(cd)

 giả sử n^2 = (abcd) = 100(ab) + (cd) = 100( 1+(cd)) + (cd) = 101(cd) +100

  đk : 31 101(cd) = n^2 -100

= (n+10)(n-10)  vì n< 100 => n-10 < 90 và 101 là số nguyên tố nên:

n+10 = 101 => n =91

  thử lại: số chính phương 91^2 = 8281

thỏa đk 82-81=1