TD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
0
14 tháng 5 2023
a) Ta có A = 1 + 4 + 42 + 43 + ... + 449
4A = 4 + 42 + 43 + 44 + ... + 450
4A - A = ( 4 + 42 + 43 + 44 + ... + 450 ) - ( 1 + 4 + 42 + 43 + ... + 449 )
3A = 450 - 1
A = \(\dfrac{4^{50}-1}{3}\)
Vì A = \(\dfrac{4^{50}-1}{3}\) < \(\dfrac{4^{100}}{3}\) = \(\dfrac{B}{3}\) nên A < \(\dfrac{B}{3}\)
b) Ta có A = 1 + 4 + 42 + 43 + ... + 449
= 1 + 4 + ( 42 + 43 + 44 ) + ( 45 + 46 + 47 ) + ... + ( 447 + 448 + 449 )
= 5 + 42( 1 + 4 + 42 ) + 45( 1 + 4 + 42 ) + ... + 447( 1 + 4 + 42 )
= 5 + 42 . 16 + 45 . 16 + ... + 447 . 16
= 5 + 21( 42 + 45 + ... + 447 )
Vì [ 21( 42 + 45 + ... + 447 )] ⋮ 21 nên A = 5 + 21( 42 + 45 + ... + 447 ) chia 21 dư 5
Vậy A chia 21 dư 5
14 tháng 5 2023
đây là toán lớp 6 ư. Ròi xong tới công chuyện với me òi năm sau lên lớp 6
AH
Akai Haruma
Giáo viên
13 tháng 12 2022
Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
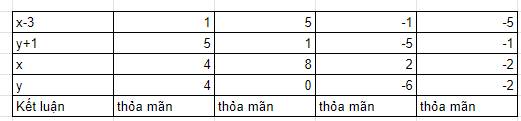
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.
TM
0
PL
4 tháng 3 2018
1/ ta có:
A = 1 - 5 - 9 + 13 + 17 - 21 - 25 + ... + 2001 - 2005 - 2009 + 2013
A = (1 - 5 - 9 + 13) + (17 - 21 - 25 + 29) + ,,,,, + (2001 - 2005 - 2009 + 2013)
A = 0 + 0 + ..... + 0
A = 0
Vậy A = 0
PL
4 tháng 3 2018
2/ Gọi số cần tìm là n
Có n : 11 dư 6 => n - 6 chia hết cho 11 => n - 6 + 33 = n + 27 chia hết cho 11 (Do 33 chia hết cho 11) (1)
Có n : 4 dư 1 => n - 1 chia hết cho 4 => n - 1 + 28 = n + 27 chia hết cho 4 (Do 28 chia hết cho 4) (2)
Có n : 19 dư 11 => n - 11 chia hết cho 19 => n - 11 + 38 = n + 27 chia hết cho 19 (Do 38 chia hết cho 19) (3)
Từ (1), (2), (3) => n + 27 chia hết cho các số 4 ; 11 ; 19 => n + 27 = BCNN(4 ; 11 ; 19) = 836
Vậy n = 836 - 27 = 809
HT
2
M
27 tháng 6 2015
Ta có: a + 19 chia hết cho 21 và 15
=> a + 19 thuộc BC(21; 15)
=> a + 19 thuộc {84; 168;...}
=> a thuộc {65; 149; ...}
Vì a nhỏ nhất => a = 65
CC
0
17 tháng 3 2020
a)Chia cho 29 dư 5 nghĩa là: A = 29p + 5 ( p ∈ N )
Tương tự: A = 31q + 28 ( q ∈ N )
Nên: 29p + 5 = 31q + 28 => 29(p - q) = 2q + 23
Ta thấy: 2q + 23 là số lẻ => 29(p – q) cũng là số lẻ =>p – q >=1
Theo giả thiết A nhỏ nhất => q nhỏ nhất (A = 31q + 28)
=>2q = 29(p – q) – 23 nhỏ nhất
=> p – q nhỏ nhất
Do đó p – q = 1 => 2q = 29 – 23 = 6
=> q = 3
b)126: a dư 25=>a khác 0 ; 1;126
=>126-25=101 chia hết cho a
Mà 101=1.101
=>a=1(L) hoặc a=101(TM)
Vậy a=101
B
17 tháng 3 2020
gọi số cần tìm là A :
chia cho 29 dư 5
A = 29 x p + 5 ( p \(\in\)N )
A = 31 x q + 28 ( q \(\in\)N )
nên :
29 x p + 5 = 31 x q + 28
=> 29 x ( p - q ) = 2 x q + 23
ta có :
2 x q + 23 là số lẻ
=> 29 x ( p - q ) là số lẻ
vậy p - q = 1
theo giả thiết phải tìm A nhỏ nhất :
=> 2q = 29 x ( p - q ) - 23 nhỏ nhất
=> q nhỏ nhất ( A = 31 x q + 28 )
=> p - q nhor nhất
suy ra : 2 x q = 29 x 1 - 23 = 6
=> q = 6 : 2 = 3
vậy số cần tìm là : A = 31 x q + 28 =31 x 3 + 28 = 131