
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(\left(3n+14\right)⋮\left(n+2\right)\\ \Rightarrow\left[\left(3n+6\right)+8\right]⋮\left(n+2\right)\\ \Rightarrow\left[3\left(n+2\right)+8\right]⋮\left(n+2\right)\)
Vì \(3\left(n+2\right)⋮\left(n+2\right)\Rightarrow8⋮\left(n+2\right)\Rightarrow n+2\in8=\left\{\pm1;\pm2;\pm4;\pm8\right\}\Rightarrow n\in\left\{-10;-6;-4;-3;-1;0;2;6\right\}\)

3n + 14 chia hết cho n + 2
⇒ 3n + 6 + 8 chia hết cho n + 2
⇒ 3(n + 2) + 8 chia hết chi n + 2
⇒ 8 chia hết cho n + 2
⇒ n + 2 ∈ Ư(8) = {1; -1; 2; -2; 4; -4; 8; -8}
⇒ n ∈ {-1; -3; 0; -4; 2; -6; 6; -10}
Mà n là số tự nhiên
⇒ n ∈ {0; 2; 6}
\(\left(3n+14\right)=3\left(n+2\right)+8\)
Để \(\left(3n+14\right)⋮\left(n+2\right)\Rightarrow\left(n+2\right)\inƯ\left(8\right)\)
\(\Rightarrow\left(n+2\right)\in\left\{-1;1;-2;2;-4;4;-8;8\right\}\)
\(\Rightarrow n\in\left\{-3;-1;-4;0;-6;2;-10;6\right\}\)


3n+14 chia hết chi n+1
=>3(n+1)+11 chia hết cho n+1
=>11 chia hết cho n+1
=>n+1 thuộc Ư(11)={1;11}
+)n+1=1=>n=0
+)n+1=11=>n=10
vậy....

n2 + 3n + 2 chia hết cho n - 3
=> n2 - 3n + 6n - 18 + 20 chia hết cho n - 3
=> (n2 - 3n) + (6n - 18) + 20 chia hết cho n - 3
=> n(n - 3) + 6(n - 3) + 20 chia hết cho n - 3
=> (n + 6)(n - 3) + 20 chia hết cho n - 3
Vì (n + 6)(n - 3) chia hết cho n - 3
=> 20 chia hết cho n - 3
=> n - 3 \(\in\)Ư(20) = {-1;1;-2;2-4;4;-5;5;-10;10;-20;20}
=> n \(\in\){2;4;1;5;-1;7;-2;8;-7;13;-17;23}
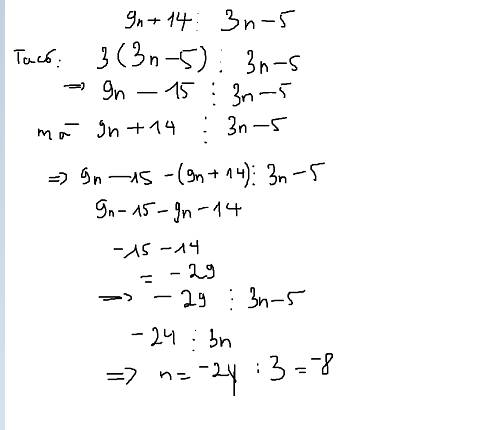

\(3n+14⋮n+2\)
\(\Rightarrow3\left(n+2\right)+8⋮n+2\)
\(\Rightarrow8⋮n+2\)
\(\Rightarrow n+2\in\text{Ư}\left(8\right)\)
\(\Rightarrow n+2\in\text{{}\pm1;\pm2;\pm4;\pm8\text{ }\)
\(\Rightarrow n\in\left\{-1;-3;0;-4;2;-6;6;-10\right\}\)