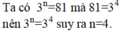Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(25< 3^x< 250\)
\(3^{2,9}< 3^x< 3^{5,02}\)
\(x=3;4;5\)

ta có: \(3^3=27\)
\(3^4=81\)
\(3^5=243\)
vậy \(x\in\left\{3;4;5\right\}\)

ta có: \(3n+25⋮3n+2\)
\(\Leftrightarrow3n+2+23⋮3n+2\)
Do \(3n+2⋮3n+2\Rightarrow23⋮3n+2\)
\(\Leftrightarrow3n+2\inƯ\left(23\right)\)
\(\Rightarrow3n+2\in\left(\pm1;\pm23\right)\)
Ta có bảng sau:
| 3n+2 | -23 | -1 | 1 | 23 |
| 3n | -25 | -3 | -1 | 21 |
| n | loại | loại | loại | 7 |
vậy n=7

do 3n+25 chia hết cho 3n+2
mà 3n+2 chia hết cho 3n+2
Nên (3n+25)-(3n+2) chia hết cho 3n+2
=>23 chia hết cho 3n+2
=>3n+2 thuộc Ư(23)={-23;-1;1;23}
( bạn tự thay số và làm tiếp nhé)
Ta có: 3n+25=3n+2+23
Vì 3n+25 chia hết 3n+2 mà 3n+2 chia hết co 3n+2 => 23 chia hết cho 3n+2
Vì n thuộc N nên 3n+2 thuộc N =>3n+2 thuộc ước của 23
Ta có bảng
| 3n+2 | 23 | 1 |
| 3n | 21 | -1 |
| n | 7(thỏa mãn) | -1/3 (không thỏa mãn) |
Vậy n=7 thì 3n+25 chia hết cho 3n+2
k cho mình nha


\(3n+11⋮n-3\)
=>\(3n-9+20⋮n-3\)
=>\(n-3\inƯ\left(20\right)\)
=>\(n-3\in\left\{1;-1;2;-2;4;-4;5;-5;10;-10;20;-20\right\}\)
=>\(n\in\left\{4;2;5;1;7;-1;8;-2;13;-7;23;-17\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{4;2;5;1;7;8;13;23\right\}\)

Bài 1: Gọi d=ƯCLN(3n+11;3n+2)
=>\(\left\{{}\begin{matrix}3n+11⋮d\\3n+2⋮d\end{matrix}\right.\)
=>\(3n+11-3n-2⋮d\)
=>\(9⋮d\)
=>\(d\in\left\{1;3;9\right\}\)
mà 3n+2 không chia hết cho 3
nên d=1
=>3n+11 và 3n+2 là hai số nguyên tố cùng nhau
Bài 2:
a:Sửa đề: \(n+15⋮n-6\)
=>\(n-6+21⋮n-6\)
=>\(n-6\in\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
=>\(n\in\left\{7;5;9;3;13;3;27;-15\right\}\)
mà n>=0
nên \(n\in\left\{7;5;9;3;13;3;27\right\}\)
b: \(2n+15⋮2n+3\)
=>\(2n+3+12⋮2n+3\)
=>\(12⋮2n+3\)
=>\(2n+3\in\left\{1;-1;2;-2;3;-3;4;-4;6;-6;12;-12\right\}\)
=>\(n\in\left\{-1;-2;-\dfrac{1}{2};-\dfrac{5}{2};0;-3;\dfrac{1}{2};-\dfrac{7}{2};\dfrac{3}{2};-\dfrac{9}{12};\dfrac{9}{2};-\dfrac{15}{2}\right\}\)
mà n là số tự nhiên
nên n=0
c: \(6n+9⋮2n+1\)
=>\(6n+3+6⋮2n+1\)
=>\(2n+1\inƯ\left(6\right)\)
=>\(2n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{0;-1;\dfrac{1}{2};-\dfrac{3}{2};1;-2;\dfrac{5}{2};-\dfrac{7}{2}\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{0;1\right\}\)