
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(y - 1/2) : (1/2 + 1/6 + 1/12 + ... + 1/90) = 1/3
(y - 1/2) : (1/1×2 + 1/2×3 + 1/3×4 + ... + 1/9×10) = 1/3
(y - 1/2) : (1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ... + 1/9 - 1/10) = 1/3
(y - 1/2) : (1 - 1/10) = 1/3
(y - 1/2) : 9/10 = 1/3
y - 1/2 = 1/3 × 9/10
y - 1/2 = 3/10
y = 3/10 + 1/2
y = 3/10 + 5/10
y =8/10 = 4/5

(y - \(\dfrac{1}{2}\)) : \(\left(\dfrac{1}{2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\right)\)= \(\dfrac{1}{3}\)
(y\(-\dfrac{1}{2}\)): \(\left(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)= \(\dfrac{1}{3}\)
\(\left(y-\dfrac{1}{2}\right):\left(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{10}\right)=\dfrac{1}{3}\)
\(\left(y-\dfrac{1}{2}\right):\dfrac{3}{10}=\dfrac{1}{3}\)
\(\left(y-\dfrac{1}{2}\right)=\dfrac{1}{10}\)
y = \(\dfrac{3}{5}\)


\(\left(y-\frac{1}{2}\right):\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}\right)=\frac{1}{3}\)
\(\Leftrightarrow\left(y-\frac{1}{2}\right):\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-...+\frac{1}{9}-\frac{1}{10}\right)=\frac{1}{3}\)
\(\Leftrightarrow\left(y-\frac{1}{3}\right):\left(1-\frac{1}{10}\right)=\frac{1}{3}\)
\(\Leftrightarrow\left(y-\frac{1}{2}\right):\frac{9}{10}=\frac{1}{3}\)
\(\Leftrightarrow\left(y-\frac{1}{2}\right)=\frac{3}{10}\)
\(\Leftrightarrow y=\frac{4}{5}\)


Ta có:
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}\)
\(=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+\frac{5-4}{4.5}+\frac{6-5}{5.6}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}\)
\(=1-\frac{1}{6}=\frac{5}{6}\)
Nên phương trình ban đầu tương đương với:
\(\frac{5}{6}=\frac{x}{6}\Leftrightarrow x=5\)

ta có : 13/20 x 20/17 < X < 11/6 x 12
13/17 < X < 33/4
X = 14/17,15/17,16/17,.........
k đúng cho mình nhé
Ta có :
\(\frac{\text{13}}{\text{20}}\text{x}\frac{\text{20}}{\text{17}}< \text{x}< \frac{\text{11}}{\text{6}}\text{x}\frac{\text{12}}{\text{1}}\) ( x ∈ N )
=> \(\frac{\text{13}}{\text{17}}< x< 22\)
=> 0,764.... < x < 22
=> x ∈ { 1 ; 2 ; 3 ; ... ; 21 }
Vậy x ∈ { 1 ; 2 ; 3 ; ... ; 21 }
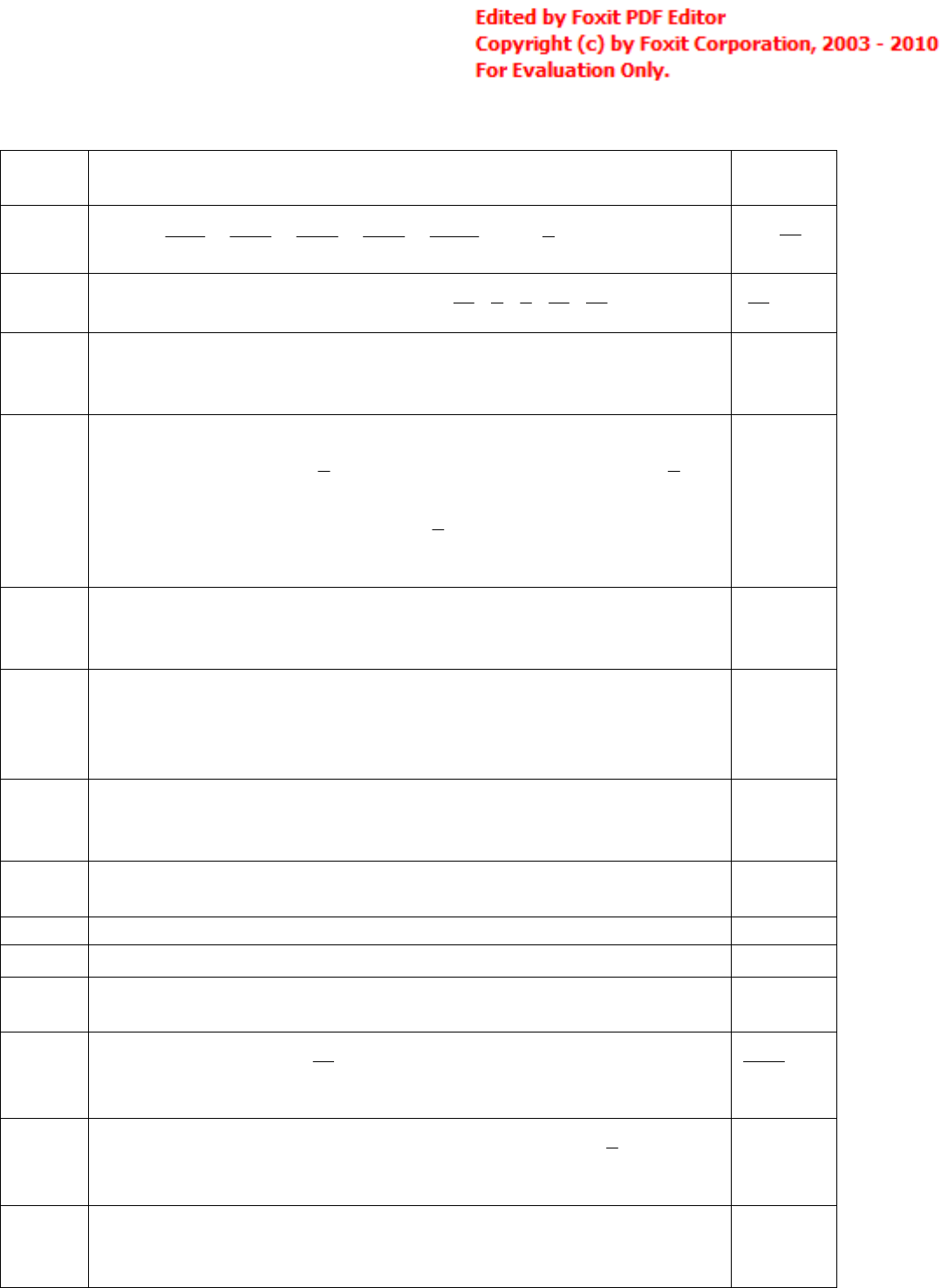 Tuyển tập đề thi vào 6 tham khảo
ĐỀ THI THỬ SỐ SỐ 20 (1)
Câu 1
Tìm số tự nhiên chia hết cho 5, biết rằng số đó cộng với hai lần tổng các chữ
số của nó thì bằng 87.
65
Câu 2
Tìm y:
1 1 1 1 1 2
1 3 3 5 5 7 7 9 9 11 3
y .
22
15
y
Câu 3
Tìm phân số lớn nhất trong các phân số sau:
9 3 5 10 21
13 4 6 11 22
; ; ; ; .
21
22
Câu 4
Tìm y:
1 1 1 1 1 2
1 3 3 5 5 7 7 9 9 11 3
y
Tuyển tập đề thi vào 6 tham khảo
ĐỀ THI THỬ SỐ SỐ 20 (1)
Câu 1
Tìm số tự nhiên chia hết cho 5, biết rằng số đó cộng với hai lần tổng các chữ
số của nó thì bằng 87.
65
Câu 2
Tìm y:
1 1 1 1 1 2
1 3 3 5 5 7 7 9 9 11 3
y .
22
15
y
Câu 3
Tìm phân số lớn nhất trong các phân số sau:
9 3 5 10 21
13 4 6 11 22
; ; ; ; .
21
22
Câu 4
Tìm y:
1 1 1 1 1 2
1 3 3 5 5 7 7 9 9 11 3
y
\(\dfrac{1}{6}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + .. + \(\dfrac{1}{90}\) = \(\dfrac{6}{y}\)
\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\)+ ... + \(\dfrac{1}{9.10}\) = \(\dfrac{6}{y}\)
\(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}-\dfrac{1}{5}\) + .. + \(\dfrac{1}{9}-\dfrac{1}{10}\) = \(\dfrac{6}{y}\)
\(\dfrac{1}{2}\) - \(\dfrac{1}{10}\) = \(\dfrac{6}{y}\)
\(\dfrac{2}{5}\) = \(\dfrac{6}{y}\)
y = 6 : \(\dfrac{2}{5}\)
y = 15
\(\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{90}=\dfrac{6}{y}\)
=>\(\dfrac{6}{y}=\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+...+\dfrac{1}{9\times10}\)
=>\(\dfrac{6}{y}=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
=>\(\dfrac{6}{y}=\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{5}{10}-\dfrac{1}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)
=>\(y=5\times\dfrac{6}{2}=15\)