Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\sqrt{x}< \sqrt{3}\Rightarrow x< 3\Rightarrow0\le x< 3\)
b) \(\sqrt{3x}< 6\Rightarrow3x< 36\Rightarrow x< 12\Rightarrow0\le x< 12\)
c) \(\dfrac{1}{2}\sqrt{5x}< 10\Rightarrow\sqrt{5x}< 20\Rightarrow5x< 400\Rightarrow x< 80\Rightarrow0\le x< 80\)

Em mới lớp 7 nên em chỉ làm những câu em biết thôi nhé:
\(a,\sqrt{x}=15\)
\(\Rightarrow x=15^2\)
\(\Rightarrow x=225\)
\(b,2\sqrt{x}=14\)
\(\sqrt{x}=14:2\)
\(\sqrt{x}=7\)
\(x=7^2\)
\(x=49\)
\(c,\sqrt{x}< \sqrt{2}\)
\(\Rightarrow x< 2\)
Còn ý d em không biết làm ạ !
\(a)\sqrt{x}=15\)
Vì \(x\ge0\) nên bình phương hai vế ta được:
\(x=15^2\Leftrightarrow x=225\)
Vậy \(x=225\)
\(b)2\sqrt{x}=14\Leftrightarrow\sqrt{x}=7\)
Vì \(x\ge0\) nên bình phương hai vế ta được:
\(x=7^2\Leftrightarrow x=49\)
Vậy \(x=49\)
\(c)\sqrt{x}< \sqrt{2}\)
Vì \(x\ge0\) nên bình phương hai vế ta được: \(x< 2\)
Vậy \(0\le x\le2\)
\(d)\sqrt{2x}< 4\)
Vì \(x\ge0\)nên bình phương hai vế ta được:
\(2x< 16\Leftrightarrow x< 8\)
Vậy \(0\le x< 8\)

`a)sqrt{x^2-2x+1}=2`
`<=>sqrt{(x-1)^2}=2`
`<=>|x-1|=2`
`**x-1=2<=>x=3`
`**x-1=-1<=>x=-1`.
Vậy `S={3,-1}`
`b)sqrt{x^2-1}=x`
Điều kiện:\(\begin{cases}x^2-1 \ge 0\\x \ge 0\\\end{cases}\)
`<=>` \(\begin{cases}x^2 \ge 1\\x \ge 0\\\end{cases}\)
`<=>x>=1`
`pt<=>x^2-1=x^2`
`<=>-1=0` vô lý
Vậy pt vô nghiệm
`c)sqrt{4x-20}+3sqrt{(x-5)/9}-1/3sqrt{9x-45}=4(x>=5)`
`pt<=>sqrt{4(x-5)}+sqrt{9*(x-5)/9}-sqrt{(9x-45)*1/9}=4`
`<=>2sqrt{x-5}+sqrt{x-5}-sqrt{x-5}=4`
`<=>2sqrt{x-5}=4`
`<=>sqrt{x-5}=2`
`<=>x-5=4`
`<=>x=9(tmđk)`
Vậy `S={9}.`
`d)x-5sqrt{x-2}=-2(x>=2)`
`<=>x-2-5sqrt{x-2}+4=0`
Đặt `a=sqrt{x-2}`
`pt<=>a^2-5a+4=0`
`<=>a_1=1,a_2=4`
`<=>sqrt{x-2}=1,sqrt{x-2}=4`
`<=>x_1=3,x_2=18`,
`e)2x-3sqrt{2x-1}-5=0`
`<=>2x-1-3sqrt{2x-1}-4=0`
Đặt `a=sqrt{2x-1}(a>=0)`
`pt<=>a^2-3a-4=0`
`a-b+c=0`
`<=>a_1=-1(l),a_2=4(tm)`
`<=>sqrt{2x-1}=4`
`<=>2x-1=16`
`<=>x=17/2(tm)`
Vậy `S={17/2}`
d.
ĐKXĐ: $x\geq 2$. Đặt $\sqrt{x-2}=a(a\geq 0)$ thì pt trở thành:
$a^2+2-5a=-2$
$\Leftrightarrow a^2-5a+4=0$
$\Leftrightarrow (a-1)(a-4)=0$
$\Rightarrow a=1$ hoặc $a=4$
$\Leftrightarrow \sqrt{x-2}=1$ hoặc $\sqrt{x-2}=4$
$\Leftrightarrow x=3$ hoặc $x=18$ (đều thỏa mãn)
e. ĐKXĐ: $x\geq \frac{1}{2}$
Đặt $\sqrt{2x-1}=a(a\geq 0)$ thì pt trở thành:
$a^2+1-3a-5=0$
$\Leftrightarrow a^2-3a-4=0$
$\Leftrightarrow (a+1)(a-4)=0$
Vì $a\geq 0$ nên $a=4$
$\Leftrightarrow \sqrt{2x-1}=4$
$\Leftrightarrow x=\frac{17}{2}$

`a)sqrt{9x^2}=6`
`<=>|3x|=6`
`<=>|x|=2`
`<=>x=+-2`
`b)sqrt{(x-2)^2}=5`
`<=>|x-2|=5`
`**x-2=5`
`<=>x=7`
`**x-2=-5`
`<=>x=-3`
`c)sqrt{x^2-6x+9}=3`
`<=>\sqrt{(x-3)^2}=3`
`<=>|x-3|=3`
`**x-3=3`
`<=>x=6`
`**x-3=-3`
`<=>x=0`
`d)sqrt{x^2+4x+4}-2x=3`
`<=>sqrt{(x+2)^2}=3+2x`
`<=>|x+2|=2x+3(x>=-3/2)`
`**x+2=2x+3`
`<=>x=-1(tm)`
`**x+2=-2x-3`
`<=>3x=-5`
`<=>x=-5/3(l)`
Sử dụng công thức:`sqrtA^2=|A|`
ĐKXĐ : \(x\in R\)
a, \(\sqrt{9x^2}=\left|3x\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=6\\3x=-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Vậy ..
b, \(\sqrt{\left(x-2\right)^2}=\left|x-2\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)
Vậy ...
c, \(\sqrt{x^2-6x+9}=\sqrt{\left(x-3\right)^2}=\left|x-3\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=3\\x-3=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=0\end{matrix}\right.\)
Vậy ..
d, \(\sqrt{x^2+4x+4}-2x=\sqrt{\left(x+2\right)^2}-2x=\left|x+2\right|-2x=3\)
\(\Leftrightarrow\left|x+2\right|=2x+3\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x+2=2x+3\\x+2=-2x-3\end{matrix}\right.\\2x+3\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{3}{2}\\\left[{}\begin{matrix}x=-1\left(TM\right)\\x=-\dfrac{5}{3}\left(L\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy ..

Với câu c, Thiên Anh nên thêm điều kiện để phần kết luận là: \(0\le x< 2.\)

\(a,ĐK:x\ge3\\ PT\Leftrightarrow x-3=5\Leftrightarrow x=8\left(tm\right)\\ b,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow2x-1=3\Leftrightarrow x=2\left(tm\right)\\ c,Vì.\sqrt{1-x}\ge0>-1.nên.pt.vô.nghiệm\\ d,PT\Leftrightarrow\left|x-1\right|=1\Leftrightarrow\left[{}\begin{matrix}x-1=1\\1-x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
a) \(\sqrt{x-3}=5\) (1)
ĐKXĐ: \(x\ge3\)
\(\left(1\right)\Leftrightarrow x-3=25\)
\(\Leftrightarrow x=28\) (nhận)
Vậy \(x=28\)
b) \(\sqrt{2x-1}=\sqrt{3}\) (2)
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
\(\left(2\right)\Leftrightarrow2x-1=3\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\) (nhận)
Vậy \(x=2\)
c) \(\sqrt{1-x}=-1\)
Không tìm được \(x\) vì \(\sqrt{1-x}\ge0\) (với mọi \(x\le1\))
d) \(\sqrt{\left(x-1\right)^2}=1\) (3)
ĐKXĐ: Với mọi \(x\in R\)
\(\left(3\right)\Leftrightarrow\left|x-1\right|=1\)
\(\Leftrightarrow x-1=1\) (khi \(x\ge1\)) hoặc \(1-x=1\) (khi \(x< 1\))
* \(x-1=1\)
\(\Leftrightarrow x=2\) (nhận)
* \(1-x=1\)
\(\Leftrightarrow x=0\) (nhận)
Vậy \(x=0;x=2\)

c) \(\sqrt{\left(x-2\right)^2}=10\)
\(x-2=10\)
\(x=12\)
d) \(\sqrt{9x^2-6x+1}=15\)
\(\sqrt{\left(3x\right)^2-2.3x.1+1^2}=15\)
\(\sqrt{\left(3x-1\right)^2}=15\)
\(3x-1=15\)
\(3x=16\)
\(x=\dfrac{16}{3}\)
a) \(đk:x\ge0\)
\(pt\Leftrightarrow3\sqrt{2x}+4\sqrt{2x}-3\sqrt{2x}=12\)
\(\Leftrightarrow4\sqrt{2x}=12\Leftrightarrow\sqrt{2x}=3\Leftrightarrow2x=9\Leftrightarrow x=\dfrac{9}{2}\left(tm\right)\)
b) \(đk:x\ge-2\)
\(pt\Leftrightarrow3\sqrt{x+2}+12\sqrt{x+2}-2\sqrt{x+2}=26\)
\(\Leftrightarrow13\sqrt{x+2}=26\)
\(\Leftrightarrow\sqrt{x+2}=2\Leftrightarrow x+2=4\Leftrightarrow x=2\left(tm\right)\)
c) \(pt\Leftrightarrow\left|x-2\right|=10\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=10\\x-2=-10\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-8\end{matrix}\right.\)
d) \(pt\Leftrightarrow\sqrt{\left(3x-1\right)^2}=15\)
\(\Leftrightarrow\left|3x-1\right|=15\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=15\\3x-1=-15\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{16}{3}\\x=-\dfrac{14}{3}\end{matrix}\right.\)
e) \(đk:x\ge\dfrac{8}{3}\)
\(pt\Leftrightarrow3x+4=9x^2-48x+64\)
\(\Leftrightarrow9x^2-51x+60=0\)
\(\Leftrightarrow3\left(x-4\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{5}{3}\left(ktm\right)\end{matrix}\right.\)

a: \(\Leftrightarrow\left|2x-3\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=7\\2x-3=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
a, \(\sqrt{\left(2x-3\right)^2}=7\\ \Rightarrow\left|2x-3\right|=7\\ \Rightarrow\left[{}\begin{matrix}2x-3=7\\2x-3=-7\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
c, \(\sqrt{x^2-9}-3\sqrt{x-3}=0\\ \Rightarrow\sqrt{x-3}\sqrt{x+3}-3\sqrt{x-3}=0\\ \Rightarrow\sqrt{x-3}\left(\sqrt{x+3}-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x+3}-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-3=0\\x+3=9\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=6\left(tm\right)\end{matrix}\right.\)
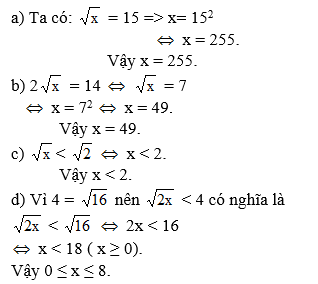
a/\(\sqrt{x}=7\)
\(\Leftrightarrow x=49\)
b/\(\Leftrightarrow x< 4\)(do x>0)
\(\Rightarrow x\varepsilon\left\{0;1;2;3\right\}\)
c/\(2x< 16\)
\(\Leftrightarrow x< 8\)
\(\Leftrightarrow x\varepsilon\left\{1;2;3;4;5;6;7\right\}\)
a) \(2\sqrt{x}=14\Leftrightarrow\sqrt{x}=7\)
\(\Leftrightarrow x=7^2\Leftrightarrow x=49\)
b) \(\sqrt{x}< \sqrt{2}\Leftrightarrow x< 2\)
c) \(\sqrt{2x}< 4\)
Vì \(4=\sqrt{16}\text{ nên }\sqrt{2x}< 4\text{ có nghĩa là }\sqrt{2x}< 16\)
\(\Leftrightarrow2x< 16\)
\(\Leftrightarrow x< 8\left(x\ge0\right)\)