Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có : -\(\sqrt{a^2+b^2}< =asinx+bcosx< =\sqrt{a^2+b^2}\)
=> \(-\sqrt{12^2+\left(-5\right)^2}< =y< =\sqrt{12^2+\left(-5\right)^2}\)
<=> \(-\sqrt{13}< =y< =\sqrt{13}\)
Vậy min=\(-\sqrt{13}\) ,max=\(\sqrt{13}\)
b) \(-\sqrt{9+16}< =3cosx-4sinx< =\sqrt{9+16}\)
<=> -5 <=3cos x -4sinx <= 5
<=> 0<= y <= 10
Vậy min=0 max=10

y=12sinx-5cosx
\(\Leftrightarrow\dfrac{y}{13}=\dfrac{12}{13}sinx-\dfrac{5}{13}cosx\) (1)
Gọi α là góc có sinα=12/13 và cosα=5/13
\(\left(1\right)\Leftrightarrow\dfrac{y}{13}=sin\left(x-\alpha\right)\)
\(\Leftrightarrow y=13sin\left(x-\alpha\right)\)
Ta có \(-1\le sin\left(x-\alpha\right)\le1\)
\(\Leftrightarrow-13\le y\le13\)
Vậy TGT của hàm số là [-13;13]

1/ \(y=\dfrac{1}{sinx-cosx}\)
Hàm số xác định khi
\(sinx-cosx\ne0\Rightarrow sinx\ne cosx\Rightarrow x\ne\dfrac{\pi}{4}+k\pi\)
2/
\(y=12sinx-5cosx=13\left(\dfrac{12}{13}sinx-\dfrac{5}{13}cosx\right)=13.sin\left(x-a\right)\)
Với góc a được xác định sao cho \(cosa=\dfrac{12}{13};sina=\dfrac{5}{13}\)
Do \(-1\le sin\left(x-a\right)\le1\Rightarrow-13\le13sin\left(x-a\right)\le13\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=-13\\y_{max}=13\end{matrix}\right.\)

\(-1< =sinx< =1\)
=>\(-3< =3\cdot sinx< =3\)
=>\(-3-2< =3\cdot sinx-2< =3-2\)
=>-5<=y<=1
Vậy: tập giá trị là T=[-5;1]

Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C

1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
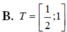

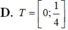
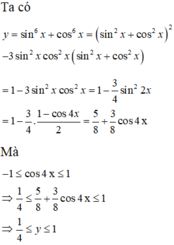
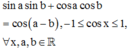
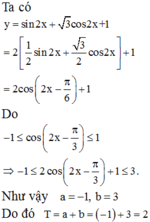
Chọn C