
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ta có: D = ℝ \ − 3 m ; y ' = 3 m 2 + 4 m − 5 x + 3 m 2 .
Để hàm số nghịch biến trên các khoảng xác định thì:
y ' < 0 ∀ x ∈ D ⇔ 3 m 2 + 4 m − 5 < 0 ⇔ − 2 − 19 3 < m < − 2 + 19 3
Vì m ∈ ℝ ⇒ m ∈ − 2 ; 1 ; 0 .
Vậy có 3 giá trị nguyên của m thỏa mãn.

Đáp án A
Điều kiện x ≥ − 2
Đặt t = x + 2 t ≥ 0 ⇒ x = t 2 − 2
Khi đó phương trình tương đương
5 − t 2 + t + 2 − 5 m = 0 ⇔ m = 5 − t 2 + t + 1
Xét hàm số f t = 5 − t 2 + t + 1 ; t ≥ 0.
Ta có:
f ' t = − 2 t + 1 5 − t 2 + t + 1 ; f ' t = 0 ⇔ t = 1 2
Từ bảng biến thiên ra suy ra phương trình có nghiệm thì 0 < m ≤ 5 5 4

Chọn đáp án B.
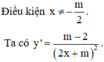
Hàm số đã cho đồng biến trên khoảng - ∞ ; - 8

Do đó, số tập con gồm 3 phần tử của tập hợp A là C 14 3 = 364

3x=3(x+1)-3 chia hết cho x+1 khi và chỉ khi 3 chia hết cho x+1.
Do đó x+1 thuộc {-3;-1;1;3}
Vậy x=-4;-2;0;2
![]()
3x=3(x+1)-3 chia hết cho x+1 khi và chỉ khi 3 chia hết cho x+1.
Do đó x+1 thuộc {-3;-1;1;3}
Vậy x=-4;-2;0;2


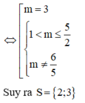




đề có sai ko bạn? Mình nghĩ phải là dấu chia hêt chứ