K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
26 tháng 3 2019
Chọn B
Đặt ![]() ,
, ![]() thì
thì ![]() .
.
Ta có:
![]()
![]()
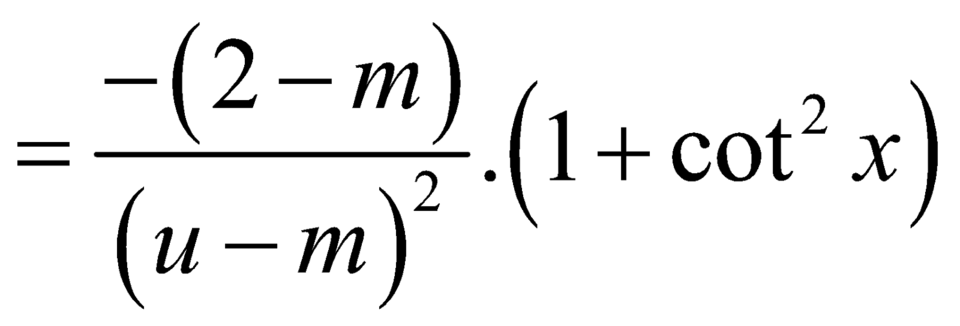 .
.
Hàm số đồng biến trên ![]()
![]()
với mọi ![]() thuộc
thuộc ![]() hay
hay 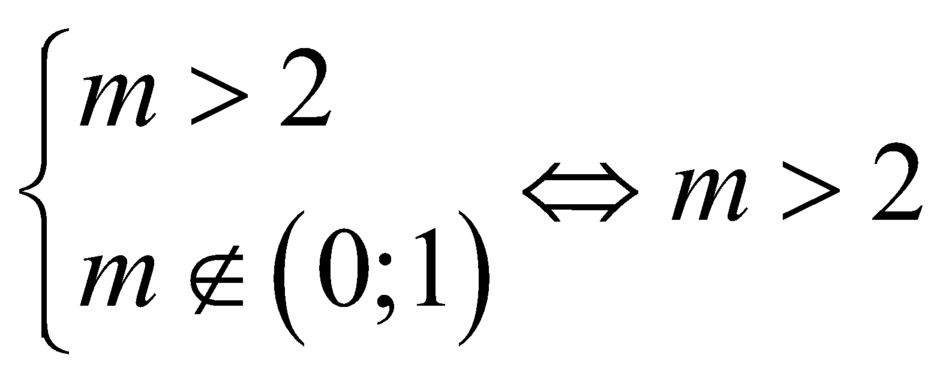 .
.

CM
12 tháng 6 2018
Chọn B
Vì trên ![]() thì
thì ![]() nhận tất cả các giá trị thuộc khoảng
nhận tất cả các giá trị thuộc khoảng ![]() nên hàm số xác trên
nên hàm số xác trên ![]() khi
khi ![]()
![]() . Ta có
. Ta có ![]() .
.
![]()
![]() . Vậy
. Vậy 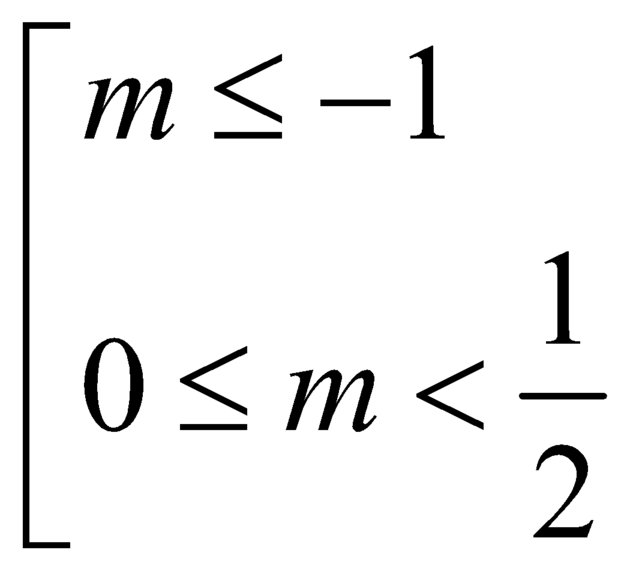 .
.

CM
2 tháng 11 2017
Chọn D.
Cách 1: Tập xác định: D = R. Ta có ![]()
+) Trường hợp 1:
![]()
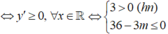
![]()
+) Trường hợp 2: Hàm số đồng biến trên (0; +∞) ⇔ y' = 0 có hai nghiệm x1; x2 thỏa mãn x1 < x2 ≤ 0(*)
-) Trường hợp 2.1: y’ = 0 có nghiệm x = 0 suy ra m = 0.
Nghiệm còn lại của y’ = 0 là x = 4 (không thỏa (*))
-) Trường hợp 2.2: y’ = 0 có hai nghiệm x1; x2 thỏa mãn:
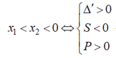
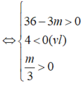
![]()
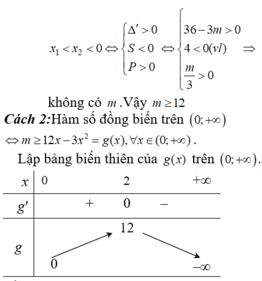
Kết hợp 2 trường hợp, vậy m ≥ 12
![]()
![]()
![]()
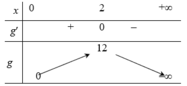
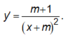
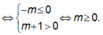


Đặt t=cotx, t>0
Ta có: y=\(\frac{t+1}{10t+m}\)
\(\Rightarrow y'=\frac{m-10}{\left(10t+m\right)^2}\)
Để hàm số đồng biến trên \(\left(0;\frac{\pi}{2}\right)\)mà hàm số t lại nghịch biến trên \(\left(0;\frac{\pi}{2}\right)\)thì m-10<0
\(\Leftrightarrow m< 10\)
Lại có điều kiện để hàm số xác định: 10t+m\(\ne0\) \(\Leftrightarrow10t\ne-m\)\(\Leftrightarrow-10t\ne m\)
Mà t>0 \(\Rightarrow-10t< 0\:\Rightarrow m\ge0\)
Vậy \(0\le m< 10\) thì hàm số đồng biến trên \(\left(0;\frac{\pi}{2}\right)\)
Không hiểu thì bạn hỏi lại mình nha ><
Đặt \(cotx=t\) \(\Rightarrow t>0\)
Ta thấy rằng khi x tăng trên \(\left(0;\frac{\pi}{2}\right)\) thì t giảm trên \(\left(0;+\infty\right)\)
Do đó hàm \(y=\frac{cotx+1}{10cotx+m}\) tăng trên \(\left(0;\frac{\pi}{2}\right)\Leftrightarrow y=\frac{t+1}{10t+m}\) giảm trên \(\left(0;+\infty\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y'=\frac{m-10}{\left(10t+m\right)^2}< 0\\-\frac{m}{10}\notin\left(0;+\infty\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 10\\-\frac{m}{10}\le0\end{matrix}\right.\) \(\Leftrightarrow0\le m< 10\)