Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(m=0\) không thỏa mãn
Với \(m\ne0\):
\(y'=4mx^3-2\left(m+1\right)x=2x\left(2mx^2-\left(m+1\right)\right)\)
Hàm có 3 cực trị khi:
\(\dfrac{m+1}{m}>0\Rightarrow\left[{}\begin{matrix}m< -1\\m>0\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m< -1\\m>0\end{matrix}\right.\)

Với \(m=-1\) thỏa mãn
Với \(m\ne-1\) hàm chỉ có cực tiểu mà không có cực đại khi:
\(\left\{{}\begin{matrix}m+1>0\\-m\left(m+1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow-1< m\le0\)
Vậy \(-1\le m\le0\)

\(y=x^4-2\left(m^2-m+1\right)x+m-1\)
\(y'=4x^3-4\left(m^2-m+1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)
Khoảng cách giữa hai điểm cực tiểu là:
\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)
Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).

Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
![]()
Hai điểm cực trị có hoành độ dương
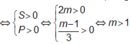
Vậy các giá trị cần tìm của m là m >1
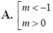
Chọn A
[Phương pháp tự luận]:
y ' = 4 m x 3 - 2 ( m + 1 ) x = 0
Hàm số có 3 điểm cực trị
[Phương pháp trắc nghiệm] :
Đồ thị hàm số y = a x 4 + b x 2 + c có 3 cực trị khi và chỉ khi a và b trái dấu , tức là : ab < 0