Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có log0,02[log2 (3x + 1)] > log0,02 m
<=> m > log2 (3x + 1) (vì cơ số = 0,02 < 1)
Xét hàm số f(x) = log2 (3x + 1) trên - ∞ ; 0
có f ' x = 3 x . ln 3 3 x + 1 ln 2 > 0 ; ∀ x ∈ - ∞ ; 0
Suy ra f(x) là hàm số đồng biến trên - ∞ ; 0
⇒ m a x - ∞ ; 0 f x = f 0 = 1
Vậy để bất phương trình có nghiệm ∀ x ∈ - ∞ ; 0 ⇒ m ≥ 1 .


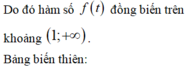
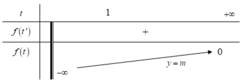
Dựa vào bảng biến thiên để phương trình có nghiệm ⇔ m < 0
Đáp án B

Đáp án A.
Phương trình
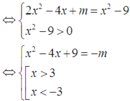
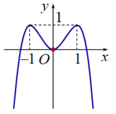
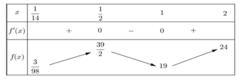
Bảng biến thiên:
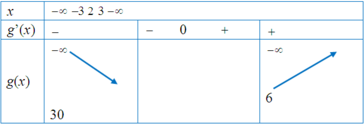
Căn cứ bảng biến thiên
=> phương trình có nghiệm khi - m > 30
<=> m < - 30

Đáp án C
Ta có : PT <=> log2 |cos x| – 2mlog|cos x| – m2 + 4 = 0
Đặt t = log|cos x|; t ∈ ( - ∞ ; 0 ]
Khi đó: t2 – 2mt – m2 + 4 = 0 (*)
PT đã cho vô nghiệm <= > (*) vô nghiệm hoặc có nghiệm dương.

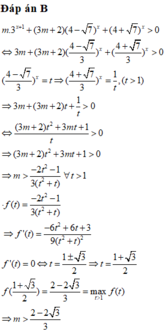




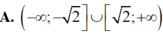



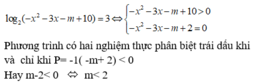
Chọn C.